Chapter 7 Red-Black Trees
Content in this chapter was originally prepared and edited by Prof Ian Sanders and Prof Hima Vadapalli.
We are looking for a data structure that allows for efficient insertion into and deletion from a “dictionary” (essentially a collection of data of some type which has order). We know that binary search trees allow insertion in \(O(\lg n)\) if the tree is balanced. Balanced binary trees also allow for deletion from the tree in \(O(\lg n)\). A red-black tree is a binary search tree with the property that it is always approximately balanced.
7.1 Summary Lecture
The video below summarises the content in this chapter. You may either watch it first, or read through the notes and watch it as a recap.
7.2 Properties
Each node in a red-black tree has the following attributes — a colour (either red or black), a key (or value), and pointers to its parent and left and right children. This is only a small change to an ordinary binary search tree node. Note that for convenience we also use “special” nodes — Nil nodes — to represent the leaves in the tree.
The trees have the following properties:
- Every node is either red or black
- The root node is always black
- Every leaf node (defined as a Nil) is black
- If a node is red then its children must be black
- Every simple path from a node to a descendant leaf contains the same number of black nodes.
The properties above result in red-black trees being “almost” balanced.
The black-height of a node \(x\) (\(bh(x)\)) is the number of black nodes on any path from (but not including) \(x\) to a leaf. The black-height of a red-black tree is the black-height of its root.
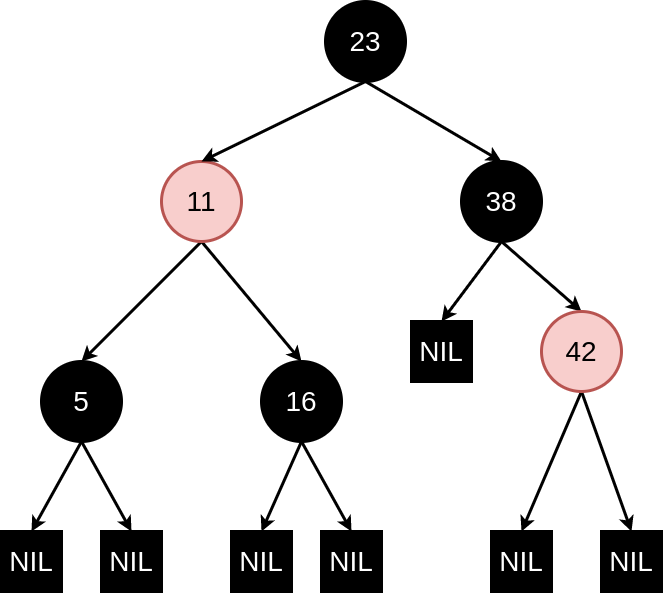
Figure 7.1: An example of a red-black tree with black-height 2
Recall that we are studying red-black trees as a data structure representing a dictionary which will allow us to do “fast” look up. Here we would want to do our look up operations in time bounded by \(\lg n\). This means that we need our red-black tree to be of height in \(O(\lg n)\). The Lemma below gives us this result.
Lemma: A red-black tree with \(n\) internal nodes has height at most \(2 \lg(n + 1)\).
Proof: We begin the proof by showing, by induction on the height of \(x\), that the subtree rooted at any node \(x\) contains at least \(2^{bh(x)} − 1\) internal nodes.
Base case: \(x\) has height \(0\), then \(x\) must be a leaf (one of the Nil nodes) and so contains \(0\) internal nodes. Also \(2^{bh(x)} − 1 = 2^0 − 1 = 1 − 1 = 0\), so the base case holds.
Induction hypothesis: Assume that any subtree of height \(\le k − 1\) rooted at some node \(y\) has at least \(2^{bh(y)} − 1\) internal nodes.
Inductive step: Let \(x\) be the root of some subtree of height \(k\), then \(x\) must be an internal node and has two chidren, \(v\) and \(w\), each of which are the roots of a sub tree of height \(\le k − 1\). By our induction hypothesis, the number of internal nodes in the subtree rooted at \(v\) is \(2^{bh(v)} − 1\) and the number of internal nodes in the subtree rooted at \(w\) is \(2^{bh(w)} − 1\). Now the black height of \(v\) and \(w\) are either \(bh(x)\) or \(bh(x) − 1\), depending on whether they are coloured red or black. Thus each of \(v\) and \(w\) have at least \(2^{bh(x)−1} − 1\) internal nodes. This means that the number of internal nodes in the subtree rooted at \(x\) is thus at least \(2^{bh(x)−1} − 1 + 2^{bh(x)−1} − 1 + 1 = 2^{bh(x)} − 1\) and the result holds by induction.
Then we let \(h\) be height of the tree. We know from the properties above that at least half of the nodes on any simple path must be black (because we can’t have two red nodes next to each other). Therefore the black-height of the tree must be at least \(h/2\). Now the tree has \(n\) internal nodes; therefore, by the property proved in the first part of the Lemma, \(n \ge 2^{h/2} − 1\) Thus \(h \le 2 \lg(n + 1)\) and the result follows.
7.2.1 Implications for Complexity
The Lemma implies that searching for a specific value in the tree, finding the minimum value in the tree, finding the maximum value in the tree, and finding the successor and the predecessor to a given node in the tree can all be done in \(O(\lg n)\) time.
We do still, however, have the problem of whether insertion and deletion can be done in \(O(\lg n)\) time. In simple binary-search trees these operations can be done in \(O(h)\) time (where \(h\) is the height of the tree). The problem is that if we insert a node into a red-black tree or delete a node from a red-black tree then we might violate the red-black properties of the tree. We would then need to adjust the tree to reestablish the red-black properties and we would need to be able to do this adjusting of the tree in a time which does not make the insertion or deletion plus adjusting of the tree more expensive than \(O(h)\) or, in the case of our “almost” balanced tree, \(O(\lg n)\).

Figure 7.2: Inserting a value into a regular Binary Search Tree
As we shall see below, we can do this and we do so by doing insertion into and deletion from red-black trees as for a normal binary search tree, but followed up by a small and strictly bounded number of rotations and colour changes to correct any violations of the red-black properties which result from the insertion or deletion. We discuss these rotations in the next section before going on to consider the insertion and deletion algorithms in detail.
7.3 Rotations
Our aim in doing rotations is to “repair” any violations to the rules of red-black trees due to inserting new nodes or deleting existing nodes, while at the same time maintaining the relationships between the nodes in the tree. First let us consider how these rotations are applied and what their effect would be. The figure below shows the right and left rotations which are used to change the shape of a given tree.
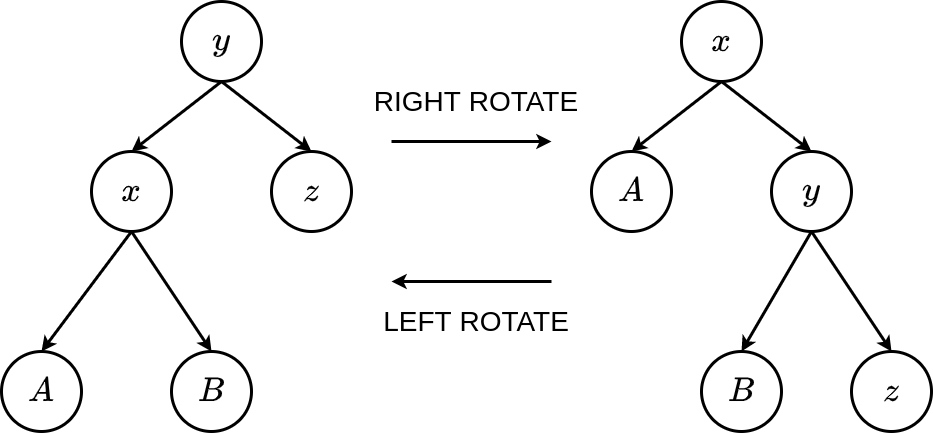
Figure 7.3: Rotations
A right rotation essentially moves the root of the current subtree down into the position in the tree previously occupied by its right child and simultaneously moves the left child into the position previously occupied by the root of the subtree. The relationships between the values stored in the nodes are maintained in the rotation. The effect of a left rotation is symmetrical. Rotations are accomplished by a few straightforward pointer changes. Note that a right rotation would be a symmetrical operation.
Note that after a rotation an inorder traversal of the tree would return the same list of numbers — the rotation does not affect the ordering in the tree. We can see this in the figure below, where a left rotation is done around the node with value \(29\). The rotation decreases the height of this subtree by \(1\), but an inorder traversal would still result in the list of numbers \(23, 26, 29, 33, 37, 51, 60\).
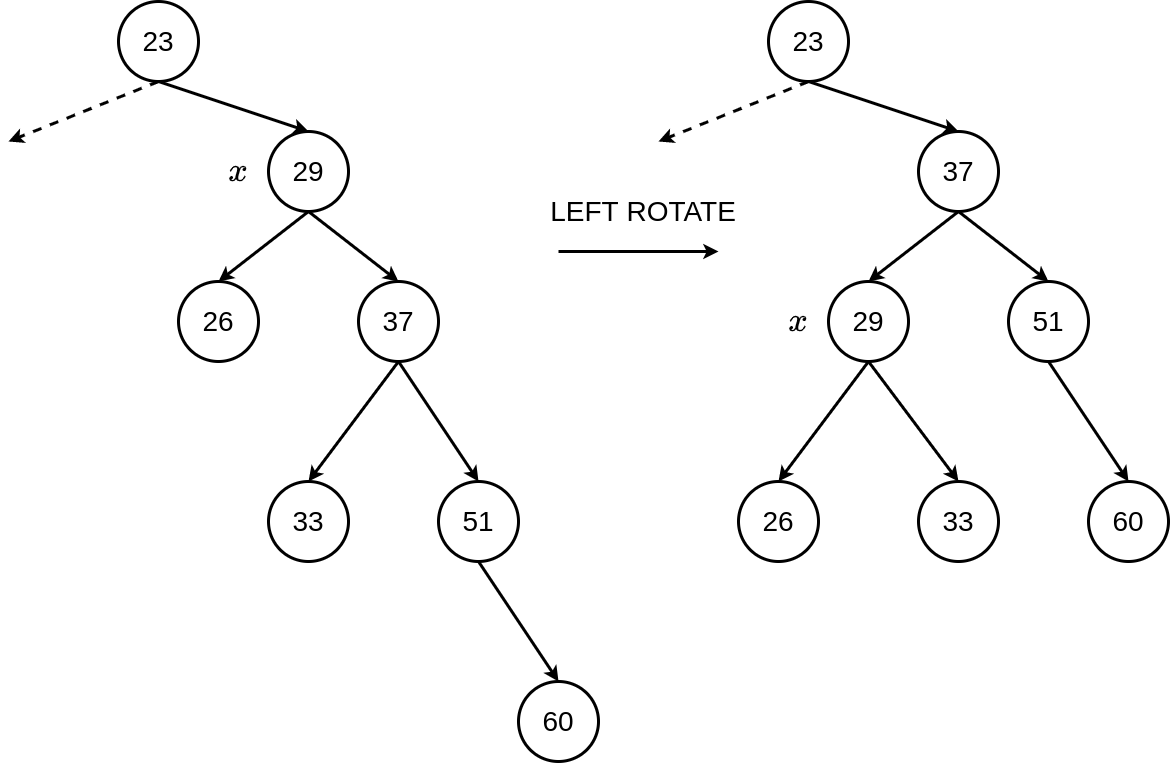
Figure 7.4: Rotations


7.4 Insertion
As discussed earlier we would use the normal tree insert algorithm to add a new node, \(z\), into the tree in the correct position in the tree based on the value to be stored in the tree. This new node would then be coloured red. After this insertion it might be necessary to fix the tree (if any of the red-black properties have been violated by the insertion).
It is in fact only possible to get a violation of property 3 — i.e. it is possible that the insertion could result in a red node with a red child. This would have to be “fixed” by rotations and recolourings.
There are only six cases in which violations of property 3 can occur. Actually there are 3 cases, with 3 symmetric cases depending on whether the parent of the node \(x\) that is added (\(x.parent\)) is a left or right child of its own parent (\(x.parent.parent\)). In the discussion that follows below we will only consider the case where \(x\)’s parent is a left child of \(x\)’s grandparent (the other case is symmetrical).
Case 1: \(x\)’s uncle/aunt is red — note that this applies whether \(x\) is the left or right child of its parent.
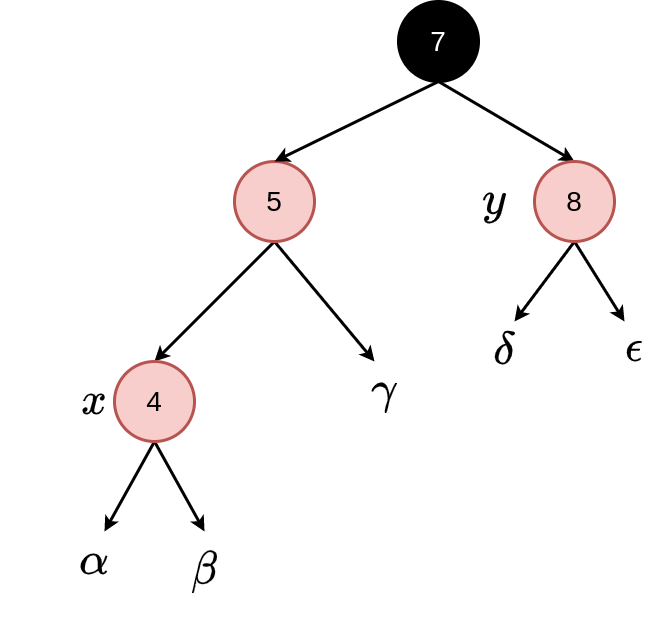
Case 2: \(x\)’s uncle/aunt is black and \(x\) is a right node of its parent.
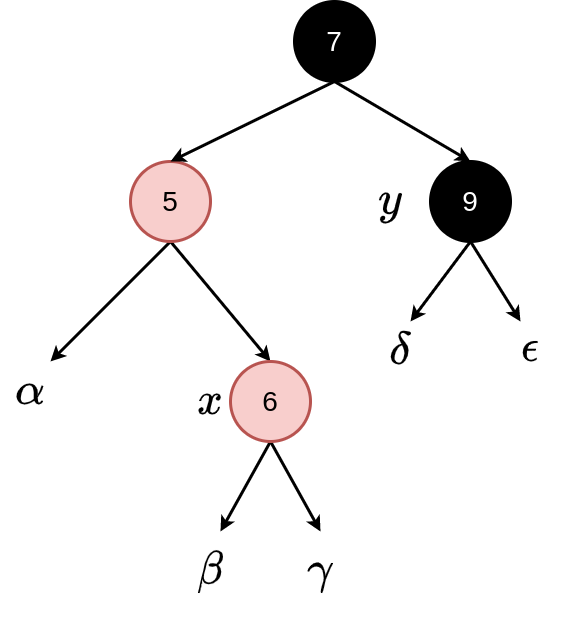
Case 3: \(x\)’s uncle/aunt is black and \(x\) is a left node of its parent
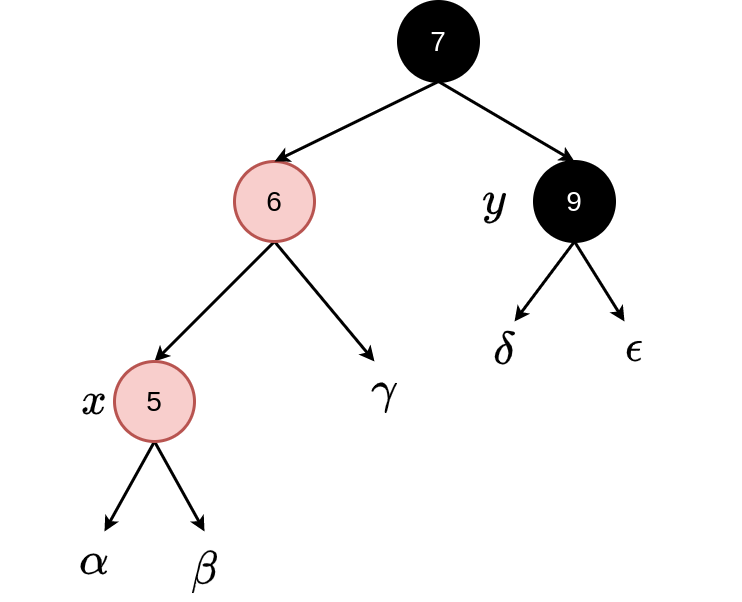
Fixing Case 1: This simply involves recolouring some nodes. Note: This could lead to a case 2 situation but only further up the tree.
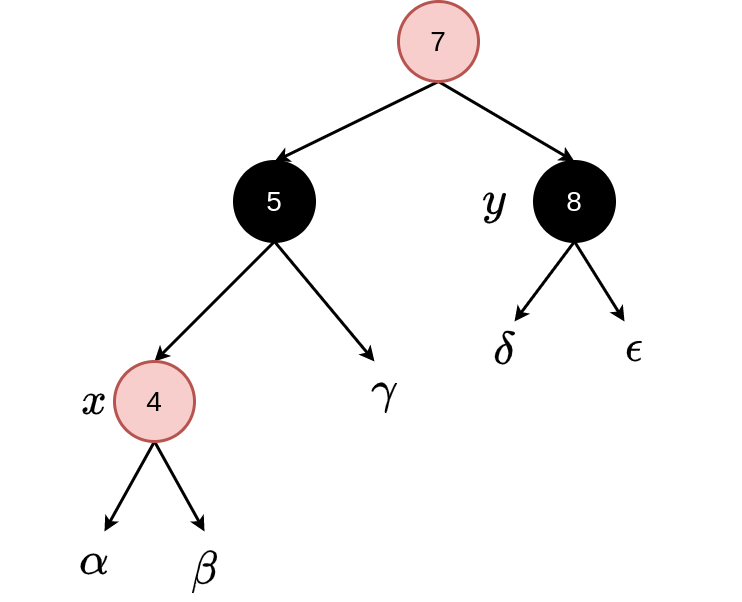
Fixing case 2: Involves a rotation (a left rotate in the case we are considering here but a right rotation if the relationship between \(x\)’s parent and \(x\)’s grandparent is different) and a relabelling of \(x\) after the rotation. Leads to case 3.
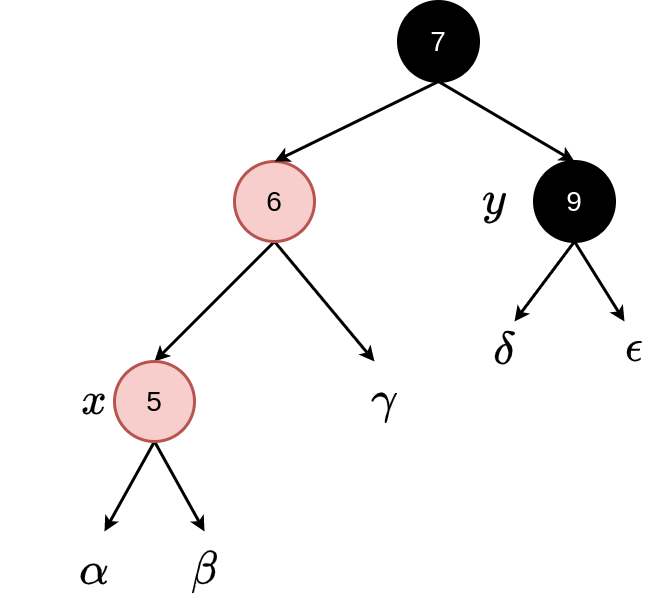
Fixing case 3: This involves some recolouring (of \(x\)’s parent and \(x\)’s grandparent) and a rotation around \(x\)’s grandparent (a right rotation in the case we are considering)
This always leads to a valid red-black tree.

Figure 7.5: Pseudocode for inserting into red-black tree
7.5 Deleting from a binary search tree
Deleting a node, \(z\), from a binary tree is relatively simple to do — there are only three cases to consider:
- If \(z\) has no children, then delete \(z\) and modify \(z.parent\) to point to Nil rather than to \(z\).
- If \(z\) has a single child, then splice out \(z\) and reset \(z.parent\) to point to the left or right child of \(z\) (whichever exists) instead of to \(z\)
- If \(z\) has two children then find \(z\)’s successor \(y\) and remove \(y\) (which will be either case 1 or 2) and then replace the contents (in the most simple case this will be only the key) of \(z\) with the contents of \(y\)
7.6 Deleting from a red-black tree
We now know that we can do insertions into a red-black tree in \(O(\lg n)\) time. For our data structure to be efficient we want deletions to also take \(O(\lg n)\) time.
As in the case of inserting into a red-black tree, deletion from a red-black tree will essentially be applying the normal tree deletion algorithm and after deleting a node repairing the tree if any of the red-black properties have now been violated. This repairing of the tree is done by changing colours and/or performing rotations to restore red-black properties.
Note that we only have a problem if the spliced out node is black, not if the spliced out node is red. Removing a black node changes the black height of some of the nodes in the tree. This violates property 4 of red-black trees.
In some situations it seems that it would be possible to fix the problem by passing the blackness to the child, say \(x\), of the deleted node. A problem arises then if such a child node becomes “double black.” This violates property 1 of red-black trees.
So our deletion algorithm has to deal with this problem by moving the “extra black” up the tree until one of the following situations occurs.
- \(x\) points to a red node. In this case we can colour the node pointed to by \(x\) black and we are done.
- \(x\) points to the root of the tree. In which case we can simply “throw away” the extra black
- It is possible to do rotations and/or recolourings to make the tree conform to the red-black properties.
Once again there are a limited number of cases which have to be dealt with by our algorithm — these four cases (eight actual cases but reduced to four by symmetry) are detailed below.
- Node \(w\), the sibling of \(x\), is red
- Node \(w\) is black and \(w.left\) and \(w.right\) is also black
- Node \(w\) is black and \(w.left\) is red and \(w.right\) is black
- Node \(w\) is black, \(w.left\) is either red or black and \(w.right\) is red
We will consider each of these cases below.
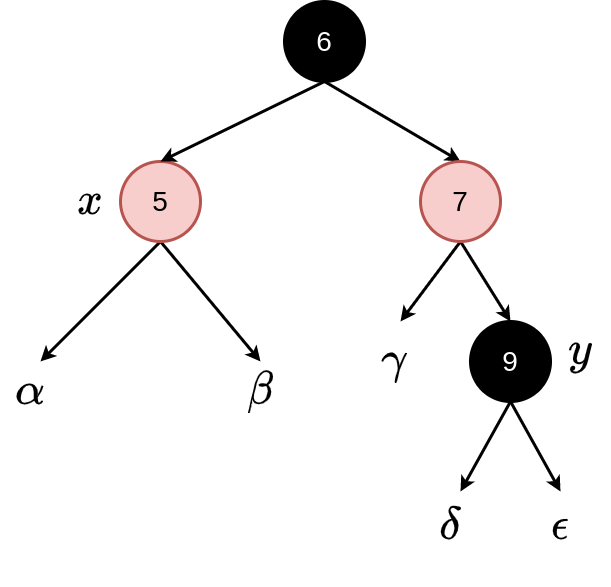
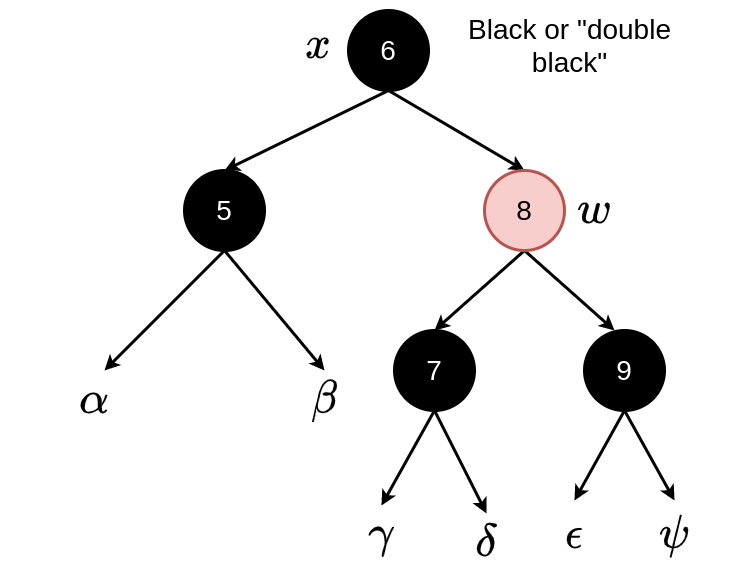
Case 1: \(w\) red, \(x\) “double black” \(\Rightarrow\) \(w\) has black children.
Switch the colours of \(w\) and \(x.parent\)
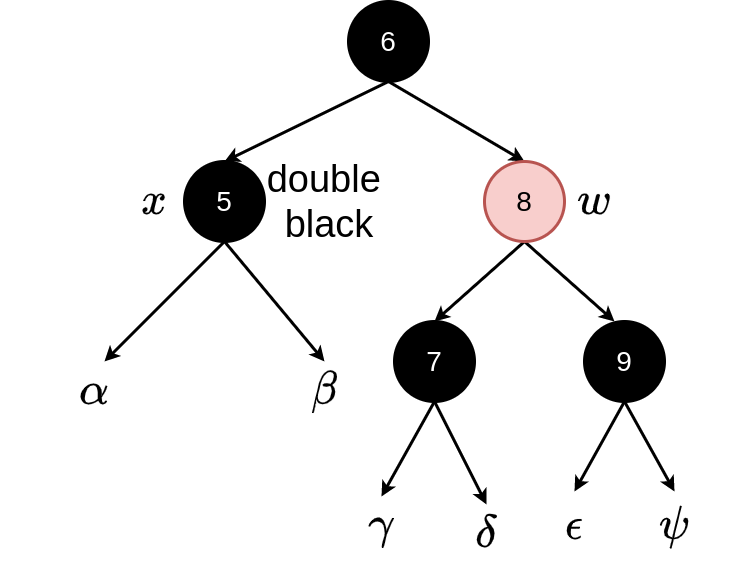
Perform a left rotation around \(x.parent\)
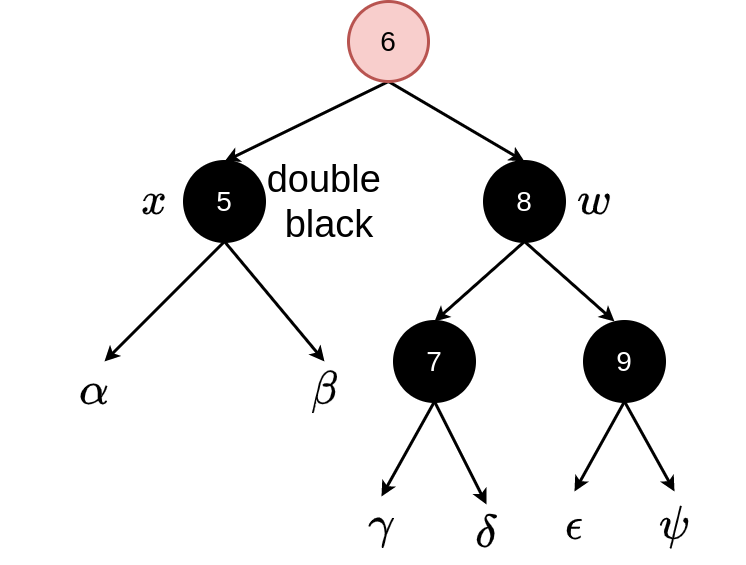
Now we have case 2, 3 or 4.
Case 2: \(w\) black, \(w.left\) and \(w.right\) black
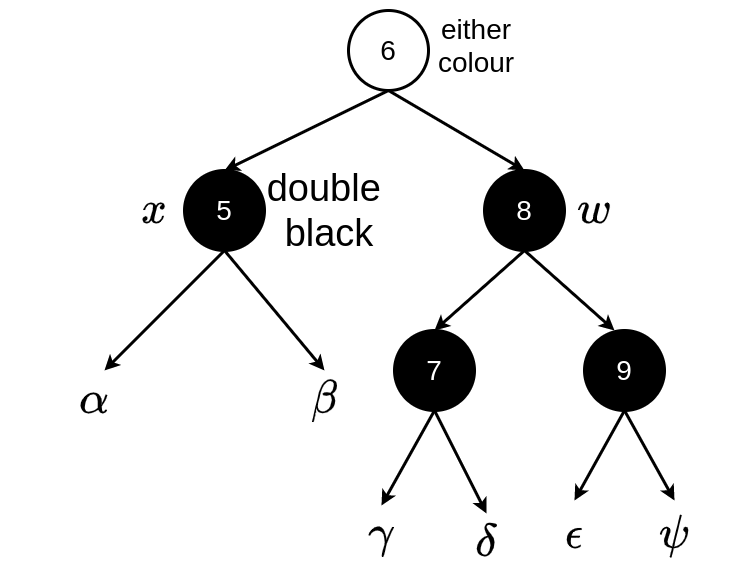
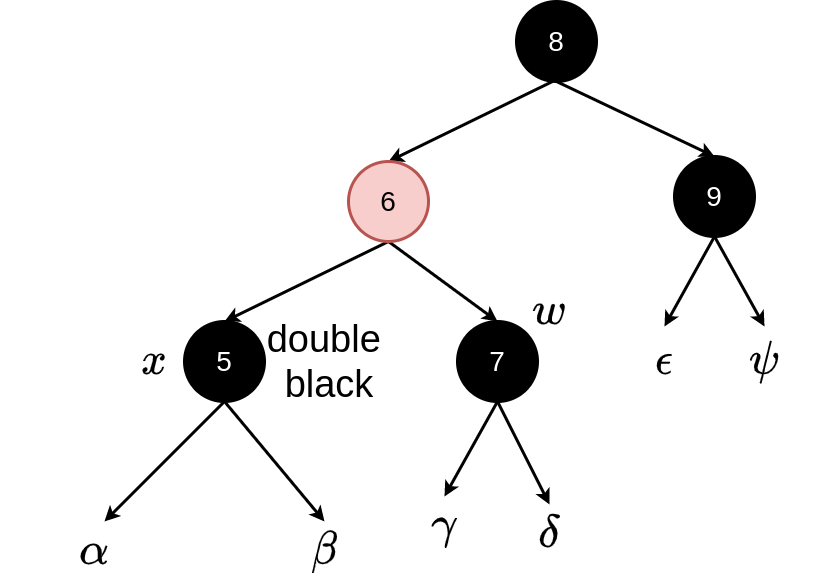
The extra black (from \(x\)) is moved up the tree by colouring \(w\) (the node with value 8) red and setting \(x\) to point to the parent of \(x\) (the node with value 6). This node could be either colour. If we entered case 2 through case 1 then it would have been red and now becomes black and the loop would terminate. If it was black it is now “double black” and we would repeat the loop.
Could lead to case 2 again or on to case 3
Case 3: \(w\) black, \(w.left\) red and \(w.right\) black
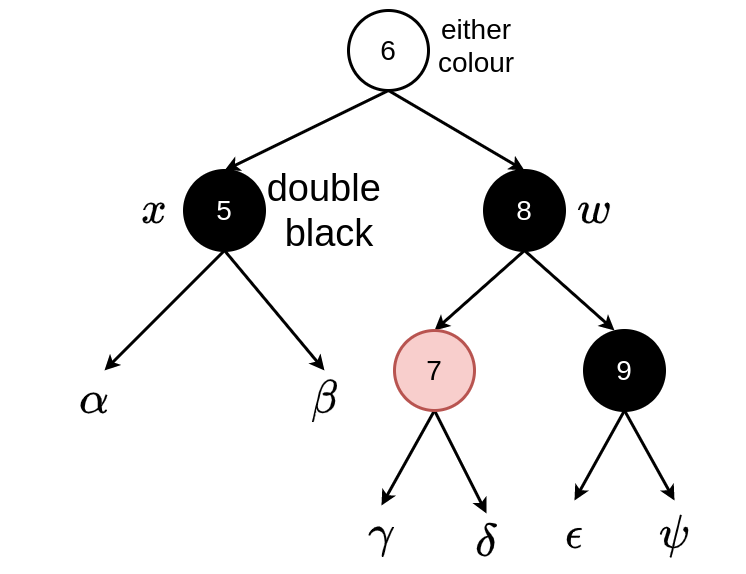
Switch colours of \(w\) and its left child
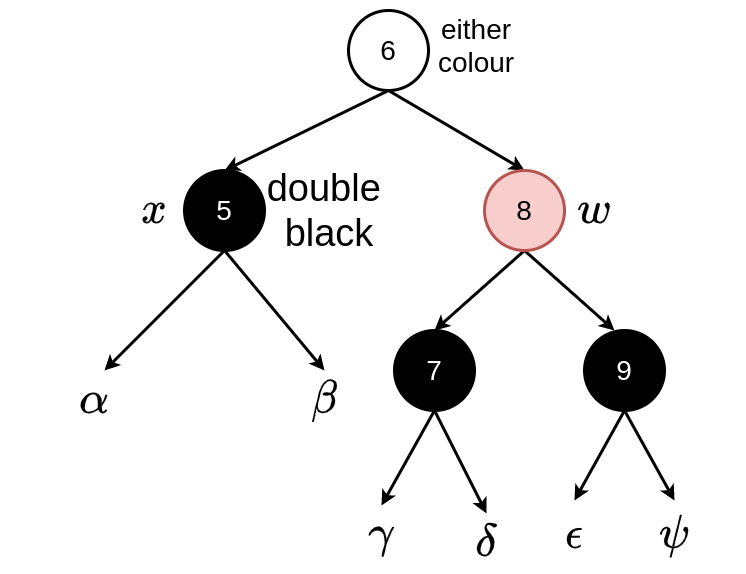
Then perform a right rotation on \(w\). This leads to case 4
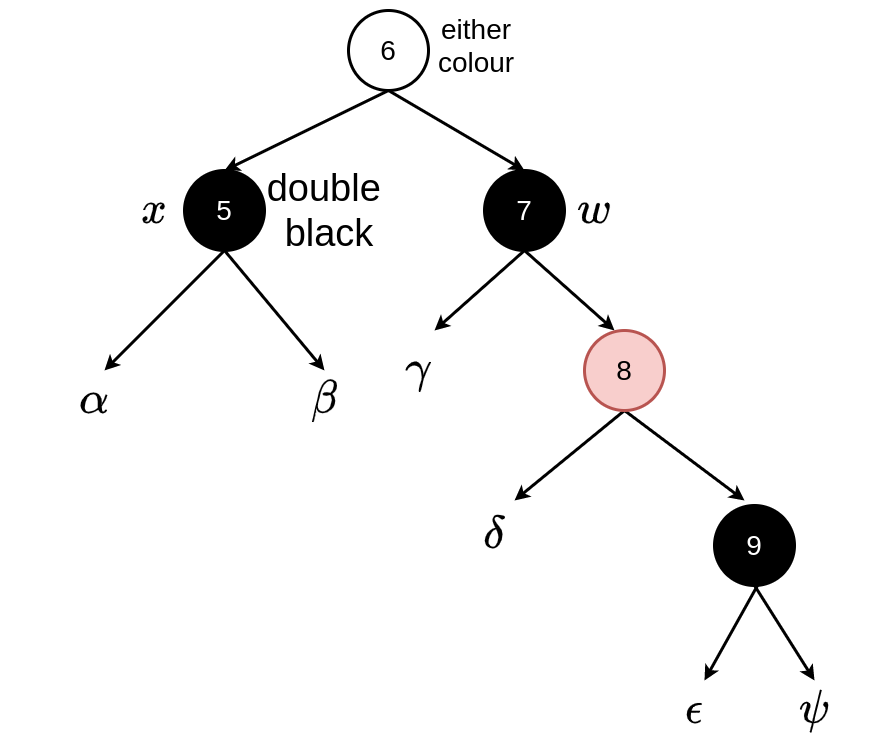
Case 4: \(w\) black, \(w.left\) any colour, \(w.right\) red
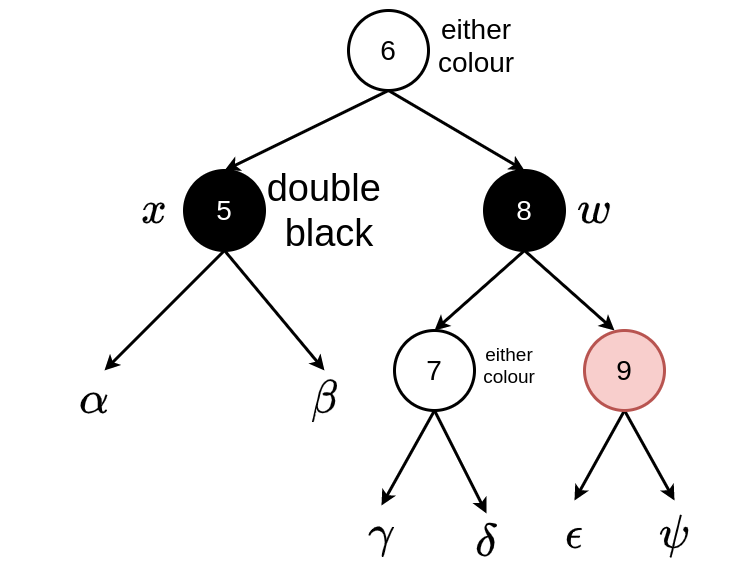
Set \(w\) to be the colour of \(x.parent\), set \(x.parent\) to be black, set colour of right child of \(w\) (\(w.right\)) to be black.
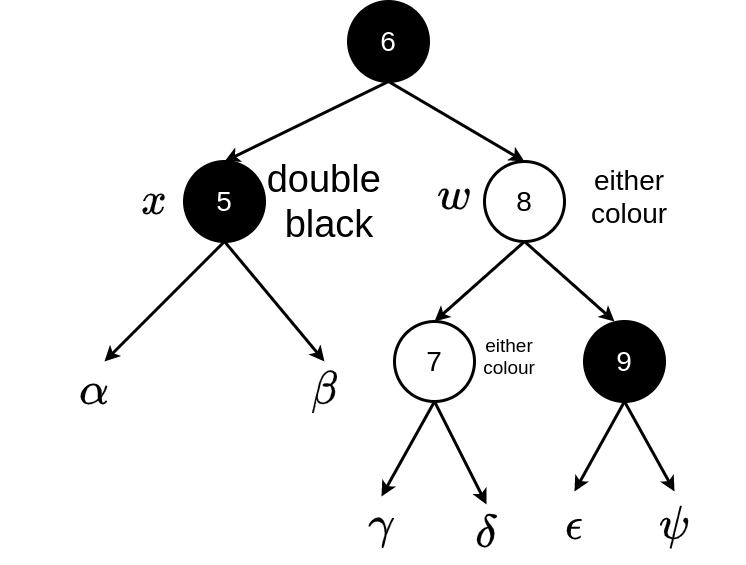
Now do a left rotation around \(x.parent\)
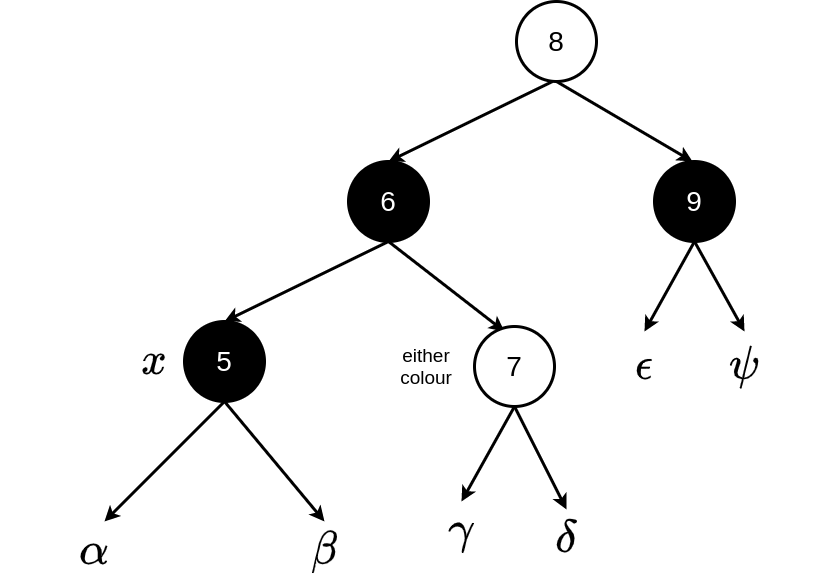
Now set \(x\) to point to the root of the tree — to force termination
In this section we have considered a data structure for a dictionary which allows us to perform a number of dictionary operations, including insertion and deletion, in time which is at worst \(O(\lg n)\). This gives us a powerful and efficient data structure which we can use in other algorithms.
7.7 Additional Reading
- Introduction to Algorithms (Chapter 14), Cormen, Leiserson, Rivest and Stein, 3rd ed.
- https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/
- https://www.codesdope.com/course/data-structures-red-black-trees-insertion/