Chapter 3 Continuous Mathematical Models

“The fact that [the model] is an approximation does not necessarily detract from its usefulness because models are approximations. All models are wrong, but some are useful.” - George E. P. Box (1919-2013)

3.1 What is Modelling?

A model is an abstraction of reality or a representation of a real object or situation. In other words, a model presents a simplified version of something. It may be as simple as a drawing of house plans, or as complicated as a miniature. It can be described as a functional representation of a complex system. A model of an airplane may be assembled and glued together from a kit by a child, or it actually may contain an engine and a rotating propeller that allows it to fly like a real airplane.

Modelling is viewed as a process or translating real-world behaviour into understandable conclusions, and there are various forms a model can take. In this Section, we will outline possible steps that can be helpful in the construction of a mathematical model. It is a useful idea to approach this with the mindset that this is a systematic or iterative process. We will often find that we missed an important factor at a later step and will have to go back to a previous step to improve the model, meaning it involves an element of refinement. The concept of trial and error is central to the modelling process and model building. We are seeking a model that is robust, but we also want to tow the line between simplicity and computational expense.

We portray the flow of the modelling process in Figure 1 below as a closed system.

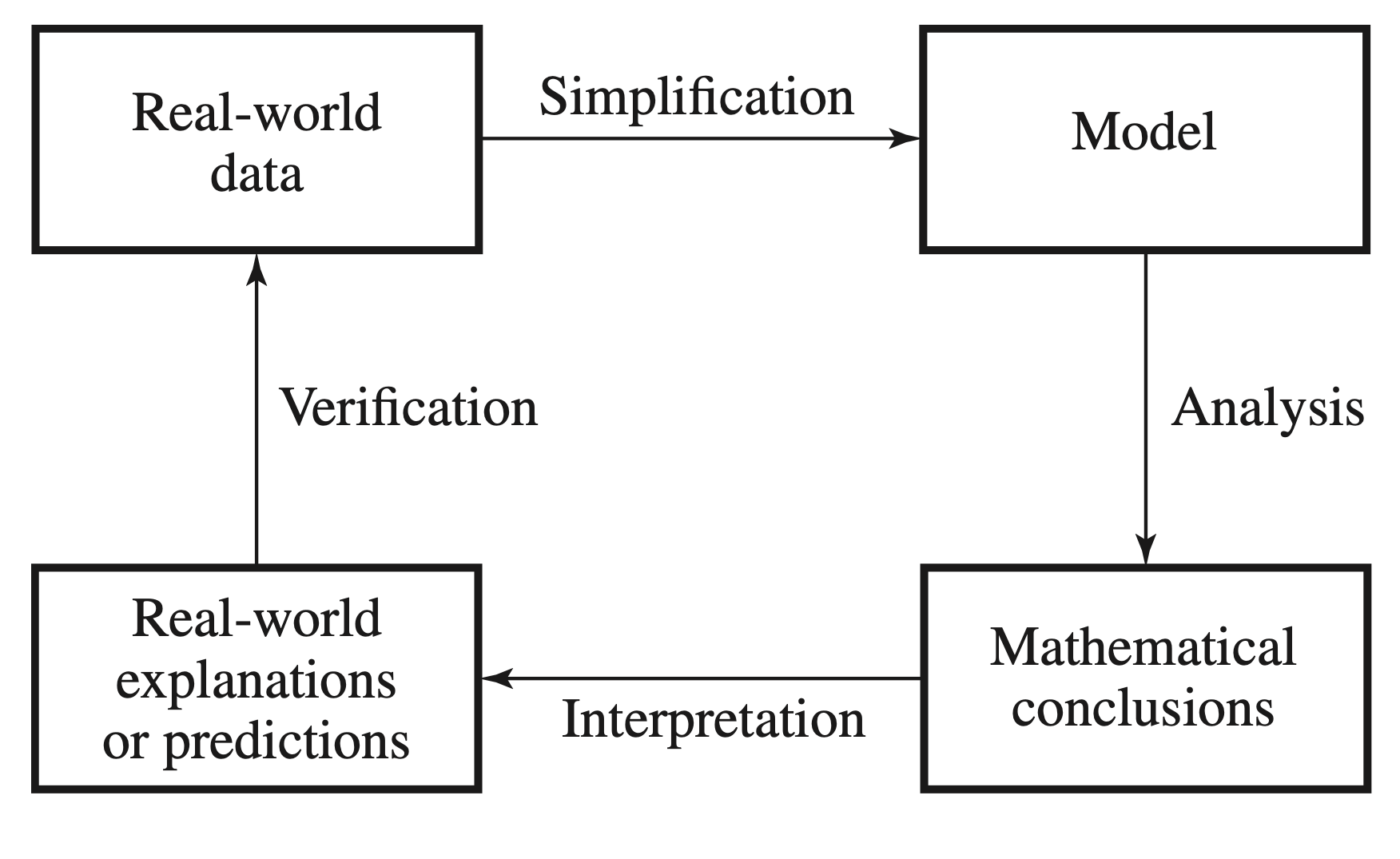
Figure 1: The modelling process as a closed system

Given some real-world system, we gather sufficient data to formulate a model. Next, we analyze the model and reach mathematical conclusions about it. Then we interpret the model and make predictions or offer explanations. Finally, we test our conclusions about the real-world system against new observations and data. We may then find we need to go back and refine the model to improve its predictive or descriptive capabilities. Or perhaps we will discover that the model really does not fit the real world accurately, so we must formulate a new model.

3.2 Mathematical Modelling

Mathematical modelling helps us in shaping real life problems into mathematical models, and then solving them accordingly. Mathematical modelling is an experimental approach where a problem is solved and continually refined over time in order to be more efficient, faster, or more accurate. It is “the process of scientific inquiry”, and it is an integral part of the toolkit of an applied mathematician.

Mathematical modelling is a principled activity that has both principles behind it and methods that can be successfully applied. The principles are overarching or meta principles phrased as questions about the intentions and purposes of mathematical modelling. These principles are almost philosophical in nature. We will now outline the principles via a visual portrayal of the basic philosophical approach in Figure 2 below.

Figure 2: A view of mathematical modelling that shows how the questions asked in a principled approach to building a model relate to the development of that model

These methodological modelling principles are also captured in the following list of questions and answers:

Why? What are we looking for? Identify the need for the model.
Find? What do we want to know? List the data we are seeking.
Given? What do we know? Identify the available relevant data.
Assume? What can we assume? Identify the circumstances that apply.
How? How should we look at this model? Identify the governing physical principles.
Predict? What will our model predict? Identify the equations that will be used, the calculations that will be made, and the answers that will result.
Valid? Are the predictions valid? Identify tests that can be made to validate the model, i.e., is it consistent with its principles and assumptions?
Verified? Are the predictions good? Identify tests that can be made to verify the model, i.e., is it useful in terms of the initial reason it was done?
Improve? Can we improve the model? Identify parameter values that are not adequately known, variables that should have been included, and/or assumptions/restrictions that could be lifted. Implement the iterative loop that we can call “model-validate-verify-improve-predict”.
Use? How will we exercise the model? What will we do with the model?

This list of questions and instructions is not an algorithm for building a good mathematical model. However, the underlying ideas are key to mathematical modelling, as they are key to problem formulation generally. Thus, we should expect the individual questions to recur often during the modelling process, and we should regard this list as a fairly general approach to ways of thinking about mathematical modelling.

3.3 The Formal Model Construction Process

As mentioned above, there is no definite algorithm to construct a mathematical model that will work in all situations. Modelling is sometimes viewed as an art. It involves taking whatever knowledge one may possess in mathematics and of the system of interest and using that knowledge to create something. Since everyone has a different knowledge base, a preferred bag of tricks, and a unique way of looking at problems, different people may come up with different models for the same system. Thus, it is very important to understand that for any real system, there is no perfect model. One is always faced with trade-offs between accuracy, flexibility, and cost. Increasing the accuracy of a model generally increases cost and decreases flexibility. The object in creating a model is usually to obtain a sufficiently accurate and flexible model at a lower cost.

We shall follow the outlined iterative process below to build and verify each model. In each iteration, we shall implement an ordered sequence of tasks, namely

Problem Identification
Assumption Specification
Variable Classification
Model Construction
Model Problematization
Model Solution
Model Interpretation, Verification, and Validity
Model Refinement, Implementation, Management, and Maintenance

Each of these exists for a specific reason, and at any point in the sequence it may be necessary to review a previous step before continuing to the next.

Let us interrogate each of these tasks in some detail.

1. Problem Identification

First, identify the problem. This amounts to asking the question “What is the problem you wish to explore?” This is usually not an easy step, since in real-life situations there is usually no one who will hand you the problem that is to be solved mathematically. This might require to sift through large amounts of data and identify some aspect of the situation to study. It is important that the problem formulation be sufficiently precise to allow for the translation of the verbal description of the problem into mathematical symbols. This process is made clear in the subsequent steps of the modelling process.

2. Assumption Specification

Once the problem is identified, the next step is to make assumptions about the problem. Usually we cannot identify all the factors affecting the problem in a usable mathematical manner. So, we must simplify the task by reducing the number of factors we need to consider to draw conclusions. Then, we must find which relationships between the remaining factors could exist in the model. This both reduces the complexity of the problem and gives us insight into which factors are necessary when drawing conclusions.

3. Variable Classification

This involves identifying all the variables, failing that, as many as possible, and listing them. Any of the variables that we want to explain are considered to be the dependent variables. There can be several dependent variables in a single model. The remaining variables are considered to be the independent variables. All the variables should be classified as dependent, independent or neither.

An independent variable may be neglected for one of two reasons. First, if the relative influence of a given independent variable is small compared to another, then we might choose to neglect it. The second reason could be that it affects the other alternatives in a similar way. An example of such variables could be bullet colour and hat size considerations when modelling wildlife hunting. While it may be an important factor in the real-life situation, it would not have much impact on the model and may add unnecessary complexity.

Next, we must determine the relationships among the remaining variables. Some problems are sufficiently complicated that identifying direct relationships is difficult. In these cases, it is productive to study some smaller model with only the variables that have obvious direct relationships. After building relationships between each sub-collection of variables, a complete and comprehensive model is built from the constituent sub-models. Considering relationships among variables such as proportionality, will aid in hypothesizing the relationships among the different variables.

4. Model Construction

Here, we use the assumptions we decided upon, as well as the way in which we classified the variables and determined the relationships among the different variables, in order to construct the model mathematically. The model can come in various forms, and may consist of mathematical equations or inequalities.

5. Model Problematization

This step involves problematizing the mathematical model we just constructed, by checking whether our model meets our expectations in terms of its behaviour. At this step, we take the model we made in the previous step and ask what the model is telling us, and whether that matches our own experiential or empirical understanding of the phenomenon.

6. Model Solution

We then try to solve the model mathematically using the techniques and methods of solution at our disposal. This step requires a solid knowledge and good understanding of solution methods available to you: you have to choose the method. Keep this in mind, and always verify your solution for errors.

The problem statement of the model could relate to finding the behaviour of a real-world situation given certain (initial) conditions, or to find the best solution, or optimal solutions to the model.

In some cases we might find at this stage that we have a model that is so complex, or vague that we cannot solve it. At this point it is often a good idea to revisit our assumptions and possibly add or replace factors. It might be necessary to redefine the problem statement entirely.

7. Model Interpretation, Verification, and Validity

The next step is to interpret, verify, and validate the model. We first begin by interpreting what the derived solution actually means, what does it tell us, and what can we infer from the solution.

The model must be properly tested before it can be used. Before embarking on this specific task, we consider whether the model does indeed supply an answer to the problem statement, and whether it is usable. If a model requires input data that is unavailable, then it is not usable. Finally, we consider whether the model is sensible.

Once a model passes these checks, it can be tested against empirical observations. The design and implementation of experiments to test a given model is outside of the scope of this course, however it is useful to add some general commentary. Tests of models should apply to the independent parameter ranges that are appropriate for the model in question. As an example, Newton’s Second Law of motion is applicable where the momentum of an object is approximately equal to the product of the mass of the object and velocity of the object. This is violated when the velocity of the object approaches the speed of light.

Note that models are approximate descriptions of a system and not necessarily a governing law. Unlike in pure Mathematics, the proof of a theorem is not merely demonstrated by a single example, but rather a general statement which requires only formal mathematical statements and is independent of physical measurement or observation. Similarly, a model can only be demonstrated to be appropriate for a given system; we cannot in general extrapolate any conclusions about a given model to broad generalizations from the evidence we gather. A model does not become law just because it is verified repeatedly in certain conditions. Instead, it is only the reasonableness of a model that is corroborated by the data we collect.

8. Model Refinement, Implementation, Management, and Maintenance

We want to explain our model in terms that the people who use the model to make decisions will understand. Furthermore, we will want to make it as simple as possible to use, otherwise these users will choose another model.

The model we have designed is often derived for a specific problem which is identified in a problem statement or from the assumptions we have made. There may be a number of reasons the model might need updating. For example, advances in measurement or data collection and availability might allow previously unknown or immeasurable factors to be included, or possibly the elimination of a previously important factor from a given model.

There are two main types of Mathematical models that we shall like to build in the chapters to follow. These are the so-called Continuous Mathematical Models that will be considered in this Chapter, and Discrete Mathematical Models in Chapter ??. For each type of model, we shall follow the same development procedure, as outlined above. We shall consider each in turn in the chapters to follow, and show the inter-relation of continuous and discrete mathematical models in different scenarios.

3.4 Conceptual and Mathematical Formulations

A conceptual formulation invariably precedes any mathematical formulation of a situation. The conceptual formulation can be expressed by means of a graph, diagram, physical model, or it can reside “purely in the mind”. We will often use rate flow diagrams or compartment models.

A verbal language is used to describe these concepts which are then translated into formal mathematical statements wherein the idea that motivates the model is made explicit in mathematical language. We shall touch briefly on this process of verbal language to mathematical language translation. We consider first the language used to describe the relationship among variables. The Table below presents these translations in detail. It shows a collection of mathematical and verbal statements describing the relationships among a collection of variables. Here, \(a\), \(b\), \(c\) and \(d\) are constants, \(k\) is a positive constant (\(k > 0\)), and \(x\), \(y\) and \(z\) are variables. We refer to \(k\) as the constant of proportionality.

Verbal Statement	Mathematical Statement
\(y\) is directly proportional to \(x\)	\(y = kx\)
\(y\) is directly proportional to the \(n\)-th power of \(x\)	\(y = k x^{n}\)
\(y\) is inversely proportional to \(x\)	\(y = \frac{k}{x}\)
\(y\) is inversely proportional to the \(n\)-th power of \(x\)	\(y = \frac{k}{x^{n}}\)
\(y\) is negatively proportional to \(x\)	\(y = - kx\)
\(z\) is proportional to \(x\) and \(y\)	\(z = k x y\)

Question: What do each of these look like graphically?

Similarly, we can describe the change in the value of a function with respect to the change in a given parameter in that function. The relationships between the relative rates of change among the dependent and independent variables are presented in the Table below, which is a collection of mathematical and verbal statements describing the relationships among a collection of variables. Here, consider a mathematical model of a physical situation where \(x\) is the dependent variable and \(t\) is the independent variable. We write this as \(x = x(t)\).

Verbal Statement	Mathematical Statement
The value of the dependent variable, \(x\), at any time \(t\)	\(x(t)\)
The rate of change of \(x\) at any time \(t\)	\(\dot x(t)\)
The rate of change of the rate of change of \(x\) at any time \(t\).	\(\ddot x(t)\)

The translation between the mathematical and verbal statements may occur explicitly and implicitly in the Sections to follow.

Modelling needs experience, which we shall gain by discussing various examples and problems. Many physical concepts, such as velocity and acceleration, describe change, and hence are represented as derivatives. Hence a model is very often an equation containing derivatives of an unknown function. Such a model is called a differential equation. Of course, we then want to find a solution (a function that satisfies the equation), explore its properties, graph it, find values of it, and interpret it in physical terms so that we can understand the behaviour of the physical system in our given problem.

Figure 3 below depicts some well-known models involving differential equations. You may have come across some of these already.

Figure 3: Some well-known models showing applications of differential equations

The next sections describes the technical aspect of describing continuous change, and how it relates to problems in mathematical modelling.

3.5 Models involving Growth

Interest in how populations tend to grow was stimulated in the late eighteenth century when Thomas Malthus (1766–1834) published “An Essay on the Principle of Population as It Affects the Future Improvement of Society”. In his book, Malthus put forth an exponential growth model for human population and concluded that eventually the population would exceed the capacity to grow an adequate food supply. Although the assumptions of the Malthusian model leave out factors important to population growth (so the model has proven to be inaccurate for technologically developed countries), it is instructive to examine this model as a basis for later refinement. It has some interesting predictions and proposed consequences that are worth discussing. Also, it is a good entry point into the world of modelling continuous change.

In this Section, we will consider various models involving population growth that build logically from each other. Commencing with the appropriate assumptions, we will construct a mathematical model that describes the growth of the world human population as a function of time, examine the model for its strengths and weaknesses and suggest modifications to the model.

Example 3.1 (Model 1 - A Simple Population Model) Suppose that the world population is increasing at a rate which is proportional to the number of people living at any particular time.

1. Problem Identification Suppose the population is \(P_{0}\) at the time \(t = t_{0}\), and we are interested in predicting the population \(P\) at some future time \(t = t_{1}\). We want to find a population function \(P(t)\) for \(t_{0} \leq t \le t_{1}\) satisfying \(P(t_{0}) = P_{0}\). Symbolically, the problem can be identified as

\[\begin{equation*} \text{Change in population} \propto \text{Population size}, \end{equation*}\] where \(\propto\) is the mathematical symbol that means “is proportional to”.

2. Assumption Specification Consider some factors that pertain to population growth. Two obvious ones are the birthrate and the death rate. The birthrate and death rate are determined by different factors. The birthrate is influenced by infant mortality rate, attitudes toward and availability of contraceptives, attitudes toward abortion, health care during pregnancy, and so forth. The death rate is affected by sanitation and public health, wars, pollution, medicines, diet, psychological stress and anxiety, and so forth. Other factors that influence population growth in a given region are immigration and emigration, living space restrictions, availability of food and water, and epidemics.

For our model, let us neglect all these latter factors. We can revise our model at a later stage if we are dissatisfied with the results. For now we will consider the birthrate and death rate to be the only factors influencing the change in the population. Because knowledge and technology have helped humankind diminish the death rate below the birthrate, human populations have tended to grow.

Let us begin by assuming that during a small time period, a percentage \(b\) of the population is newly born, and a percentage \(c\) of the population dies, i.e.

\[\begin{equation*} \text{New population} = \text{Old population}+\text{Number of births}-\text{Number of deaths} \end{equation*}\]

In other words, the new population \(P(t + \Delta t)\) is the old population \(P(t)\) plus the number of births minus the number of deaths during the time period \(\Delta t\). Symbolically, \[\begin{equation*} P(t + \Delta t) = P(t) + b P(t)\Delta t - c P(t) \Delta t, \end{equation*}\] or \[\begin{equation*} \dfrac{\Delta P}{\Delta t} = b P - c P = (b - c) P. \end{equation*}\]

3. Variable Classification Let \(P\) be the population at some point in time \(t\) such that \(P=P(t)\).

4. Model Construction From our assumptions, the average rate of change of the population over an interval of time is proportional to the size of the population. Along with our assumptions and variable classification, we can use instantaneous rate of change to approximate the average rate of change, i.e. \(\frac{\Delta P}{\Delta t} \approx \frac{\textrm{d} P}{\textrm{d}t}\), to get

\[\begin{equation*} \dfrac{\textrm{d} P}{\textrm{d}t} = (b-c) P. \end{equation*}\]

We can now take \(k=b-c\), where \(b > c\), and thus we have the following differential equation model. We need to solve \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = k P, \tag{3.1} \end{equation}\] subject to \[\begin{equation*} P(t_{0}) = P_{0}, \end{equation*}\] where \(t_{0} \leq t \leq t_{1}\), and \(k\) is a positive constant \(k > 0\) and is referred to here as a growth constant. Equation (3.1) is a first-order linear ordinary differential equation with constant coefficients, and is referred to as the Malthusian model. It is a simple population growth model, as posited by Malthus in 1798. This model neglects some important factors that influence the change in the population and those that are relevant to population growth, and this in turn limits its applicability.

5. Model Problematization Consider the Malthusian model in Equation (3.1), and check whether this model meets our expectations.

If \(P > 0\), then \(\frac{\textrm{d} P}{\textrm{d}t} > 0\), since \(k > 0\).
If \(P < 0\), then \(\frac{\textrm{d} P}{\textrm{d}t} < 0\), since \(k > 0\). (Does this make sense? Should we not check instead the case when \(P=0)\)?

Thus, our model does exhibit the expected behaviour that the change in the population is proportional to the size of the population.

6. Model Solution We can separate the variables and rewrite (3.1) by moving all terms involving \(P\) and \(\textrm{d} P\) to one side of the equation and all terms in \(t\) and \(\textrm{d} t\) to the other. This gives, \[\begin{equation*} \dfrac{ \textrm{d} P}{P} = k \textrm{d} t. \end{equation*}\] Integration of both sides of this last equation yields \[\begin{equation} \tag{3.2} \ln{P} = k t + c, \end{equation}\] for some constant \(c\). Applying the initial condition \(P(t_{0}) = P_{0}\) to (3.2) to find \(c\) results in \[\begin{equation*} \ln{P_{0}} = k t_{0} + c, \end{equation*}\] or \[\begin{equation*} c = \ln{P_{0}} - k t_{0}. \end{equation*}\] Then, substitution for \(c\) into (3.2) gives \[\begin{equation*} \ln{P} = k t + \ln{P_{0}} - k t_{0}. \end{equation*}\] or, simplifying algebraically, \[\begin{equation*} \ln{\frac{P}{P_{0}}} = k (t - t_{0}). \end{equation*}\] Finally, by exponentiating both sides of the preceding equation and multiplying the result by \(P_0\), we obtain the solution \[\begin{equation} \tag{3.3} P(t) = P_{0} e^{k (t - t_{0})} \end{equation}\]

Equation (3.3) is known as the Malthusian model of population growth, and predicts that the population grows exponentially with time.

Thinking Question: Is the above the only method of solution for Equation (3.1)?

7. Model Interpretation, Verification, and Validity The above Malthusian model (3.1) can also be solved computationally for ranging values of the growth constant \(k=0;0.5;1;1.5;2\). The code and plot is shown below:

The blue line represents when \(k=0\), and thus it is clear to see that the population \(P\) remains constant in the absence of growth.
The orange, green, red, and purple lines represent when \(k>0\), and it is clear that the population grows exponentially, and the rate of this growth is dependent on the value of the growth constant \(k\).

Because \(\ln{\frac{P}{P_{0}}} = k (t - t_{0})\), this model predicts a linear relationship between \(\ln{\frac{P}{P_{0}}}\) and \(t - t_{0}\). This means that a graph showing the relationship between \(t - t_{0}\) on the horizontal axis and \(\ln{\frac{P}{P_{0}}}\) on the vertical axis would be given by a straight line, passing through the origin with slope \(k\). However, a plot the population data for an industrially developed country over a time interval of several years is not well described by this model. For example, the \(1990\) census for the population of the United States was \(248710000\) and in 1970 it was \(203211926\). Substituting these values into (3.3) and dividing the first result by the second gives \[\begin{equation*} \frac{248710000}{203211926} = e^{k (1990 - 1970)}. \end{equation*}\] Thus, \[\begin{equation*} k = \frac{1}{20} \ln{\frac{248710000}{203211926}} \approx 0.01. \end{equation*}\] That is, during the \(20\)-year period from \(1970\) to \(1990\), the population in the United States increased at an average rate of \(1\%\) per year. Using this information with (3.3) to predict the population for the year \(2000\), where \(t_{0} = 1990\), \(P_{0} = 248710000\) and \(k = 0.01\) yields \[\begin{equation*} P(2000) = 248710000 e^{0.01 (2000 - 1990)} = 274867059. \end{equation*}\] The \(2000\) census for the population of the United States was \(281400000\) (rounded to the nearest thousand). This prediction is off by approximately \(2.4\%\). An error of this magnitude may be acceptable, and it might not be worth correcting when only short time scales are considered, However a simple calculation shows that this model predicts a population of \(5.5209\) billion in the year \(2300\) (Check this).

8. Model Refinement, Implementation, Management, and Maintenance This prediction is clearly wrong since it exceeds the sustainable carrying capacity of the entire planet. Therefore, we conclude that this model is unreasonable over long time intervals. Clearly, this model requires some refinement to make more sensible predictions. This can be done by taking into account the factors that might reduce the population growth rate over long time-intervals. These limiting factors might include limitations on the carrying capacity of the population, on food production, and other resources.

From the above, it is clear that the population grows exponentially without reaching a stable point. This is not reasonable as such a population will grow indefinitely.

We thus refine the above Malthusian Model 3.1 to incorporate the concept of a carrying capacity, which is the maximum number that the population can reach. We do this in Model 3.2 below.

Example 3.2 (Model 2 - Refining the Model to incorporate a Carrying Capacity) Suppose now that the population increases at a rate which is proportional to the difference between the current population size and the maximum possible size the population could attain.

1. Problem Identification Suppose again that the population is \(P_{0}\) at the time \(t = t_{0}\), and we are interested in predicting the population \(P\) at some future time \(t = t_{1}\). We want to find a population function \(P(t)\) for \(t_{0} \leq t \le t_{1}\) satisfying \(P(t_{0}) = P_{0}\). Symbolically, the problem can be identified either as

\[\begin{equation*} \text{Change in population} \propto (\text{Current population size} - \text{Carrying capacity}), \end{equation*}\] or \[\begin{equation*} \text{Change in population} \propto (\text{Carrying capacity}-\text{Current population size}). \end{equation*}\]

2. Assumption Specification We consider the same assumptions as in Model 3.1.

3. Variable Classification Again, let \(P\) be the population at some point in time \(t\) such that \(P=P(t)\), and let \(M\) be the maximum possible size of the population (known as the carrying capacity).

4. Model Construction Along with our assumptions and variable classification, we can consider the following two models. We need to solve \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = k(P-M), \tag{3.4} \end{equation}\] or \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = k(M-P), \tag{3.5} \end{equation}\] where \(k\) is a positive constant \(k > 0\), and is referred to here as a growth constant.

We now need to question whether Equation (3.4) or Equation (3.5) is the correct formulation.

Pause here and see if you can determine this for yourself.

5. Model Problematization Now we need to consider each of the proposed models in Equations (3.4) and (3.5), and check which of these two models meets our expectations.

First, let us consider the scenario when the carrying capacity is greater than the current population size, i.e. \(M > P\). In this scenario, our population can still grow to the carrying capacity and thus we expect population growth, i.e. \(\frac{\textrm{d} P}{\textrm{d}t}>0\) (a positive growth rate).

In Equation (3.4), if \(M>P\), it means that \(P-M <0\). We know that \(k > 0\), and so it follows that \(\frac{\textrm{d} P}{\textrm{d}t} < 0\). This does not make intuitive sense.
In Equation (3.5), if \(M>P\), it means that \(M-P >0\). We know that \(k > 0\), and so it follows that \(\frac{\textrm{d} P}{\textrm{d}t} > 0\). This makes intuitive sense.

Now, let us consider the scenario when the carrying capacity is less than the current population size, i.e. \(M < P\). In this scenario, our current population exceeds the carrying capacity and has to decreases until it reaches the carrying capacity, and thus we expect population decay, i.e. \(\frac{\textrm{d} P}{\textrm{d}t}<0\) (a negative growth rate).

In Equation (3.4), if \(M<P\), it means that \(P-M >0\). We know that \(k > 0\), and so it follows that \(\frac{\textrm{d} P}{\textrm{d}t} > 0\). This does not make intuitive sense.
In Equation (3.5), if \(M<P\), it means that \(M-P <0\). We know that \(k > 0\), and so it follows that \(\frac{\textrm{d} P}{\textrm{d}t} < 0\). This makes intuitive sense.

So based on these observations, we choose the model in Equation (3.5) and reject the model in Equation (3.4), i.e. Solve \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = k(M-P), \tag{3.6} \end{equation}\] subject to \[\begin{equation*} P(t_{0}) = P_{0}, \end{equation*}\] where \(k\) is a positive constant \(k > 0\), and is referred to here as a growth constant.

Thus, this model does (3.6) exhibits the expected behaviour that the change in the population is proportional to the difference between the current population size and the maximum possible size the population could attain.

6. Model Solution We can separate the variables and rewrite (3.6) by moving all terms involving \(P\) and \(\textrm{d} P\) to one side of the equation and all terms in \(t\) and \(\textrm{d} t\) to the other. This gives, \[\begin{equation*} \dfrac{ \textrm{d} P}{M-P} = k \textrm{d} t. \end{equation*}\] Integration of both sides of this last equation yields \[\begin{equation*} -\ln{(M-P)} = k t + c, \end{equation*}\] for some constant \(c\). \[\begin{equation*} \ln{(M-P)} = -k t + c. \end{equation*}\] Exponentiating both sides gives \[\begin{equation*} M-P = Ae^{-k t}, \end{equation*}\] which gives the general solution \[\begin{equation*} P(t) = M-Ae^{-k t}. \tag{3.7} \end{equation*}\] Applying the initial condition \(P(t_{0}) = P_{0}\) to (3.7) to find \(A\) results in \[\begin{equation*} P_{0} = M-Ae^{-k t_{0}}, \end{equation*}\] or \[\begin{equation*} A = (M-P_{0})e^{k t_{0}}. \end{equation*}\] Then, by substituting for \(A\) into (3.7), we obtain the solution \[\begin{equation} P(t) = M-(M-P_{0}) e^{-k (t-t_{0})} \tag{3.8} \end{equation}\]

Thinking Question: Is the above the only method of solution for Equation (3.6)?

7. Model Interpretation, Verification, and Validity The above modified Malthusian model with a carrying capacity (3.6) can also be solved computationally for the initial population \(P_0=100\), the growth constant \(k=5\), and ranging values of the carrying capacity \(M=50;100;150;200\). The code and plot is shown below:

The orange line represents when the initial population is the same as the carrying capacity, i.e \(M=P=100\). It is clear to see that the population \(P\) remains constant in this case, i.e. \(\frac{\textrm{d} P}{\textrm{d}t} = 0\).
The red and green lines represent when the population growth is reaching the carrying capacity of \(200\) and \(150\) respectively. It is clear to see that the population \(P\) is growing to the carrying capacity, i.e. \(\frac{\textrm{d} P}{\textrm{d}t} > 0\). Notice that the population stabilizes as it reaches the carrying capacity, i.e. it no longer grows exponentially as there is now a limiting factor for the population.
The blue line represents when the population decays until it reaches the carrying capacity of \(50\). It is clear to see that the population \(P\) is decreasing or decaying to the carrying capacity, i.e. \(\frac{\textrm{d} P}{\textrm{d}t} < 0\). Notice that the population stabilizes as it reaches the carrying capacity, i.e. it no longer decays exponentially as there is now a limiting factor for the population.

Let us consider what happens when the population is the same as the carrying capacity in the model described by Equation (3.6), i.e. \(P=M\). Thus, \[\begin{equation*} \dfrac{\textrm{d} P}{\textrm{d}t} = k(M-M)=0. \end{equation*}\] Thus, \[\begin{equation*} P(t) = c, \end{equation*}\] where \(c\) is an arbitrary constant.

This tells us that when the population reaches the carrying capacity, the rate at which the population is changing is zero. This makes sense as the when the population reaches the carrying capacity, the population stabilizes to the carrying capacity and there is no longer any population growth.

Let us now consider what happens when the population is zero in the model described by Equation (3.6), i.e. \(P=0\). Thus, \[\begin{equation*} \dfrac{\textrm{d} P}{\textrm{d}t} = k(M-P)=kM. \end{equation*}\] Thus, \[\begin{equation*} P(t) = kMt+c, \end{equation*}\] where \(c\) is an arbitrary constant.

This implies that with a population of zero, the population is still increasing linearly. There is clearly a deficiency in the model as this does not make logical sense: the model breaks down when \(P=0\).

8. Model Refinement, Implementation, Management, and Maintenance It is clear from the above analysis that Model 3.2 is also not reasonable when \(P=0\), because the growth rate for a small population is too large.

Some populations do grow exponentially, provided that the population is not too large. In most populations, however, individual members eventually compete with one another for food, living space, and other natural resources.

We account for this in Model 3.3 by refining Model 3.2 to account for limited growth and to reflect this competition.

Example 3.3 (Model 3 - Refining the Model to Reflect Limited Growth) Suppose now that the population increases at a rate which is proportional to the current population size and the difference between the current population size and the maximum possible size the population could attain.

\[\begin{equation*} \text{Change in population} \propto [\text{Current population} \times (\text{Current population} - \text{Carrying capacity})], \end{equation*}\] or \[\begin{equation*} \text{Change in population} \propto [\text{Current population} \times (\text{Carrying capacity}-\text{Current population})], \end{equation*}\]

2. Assumption Specification We consider the same assumptions as in Model 3.1.

4. Model Construction Along with our assumptions and variable classification, we can consider the following two models. We need to solve \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = kP(P-M), \tag{3.9} \end{equation}\] or \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = kP(M-P), \tag{3.10} \end{equation}\] where \(k\) is a positive constant \(k > 0\), and is referred to here as a growth constant.

We now need to question whether Equation (3.9) or Equation (3.10) is the correct formulation.

5. Model Problematization Now we need to consider each of the proposed models in Equations (3.9) (3.10), and check which of these two models meets our expectations. Go through the same steps as in Model 3.2 to determine this for yourself.

Based on your observations, you should have chosen the model in Equation (3.10) and reject the model in Equation (3.9), i.e. as a second attempt, it is reasonable to incorporate some limiting factors to the Malthusian population model with a carrying capacity in Model 3.2 to reflect the limitation on population growth. Solve \[\begin{equation} \dfrac{\textrm{d} P}{\textrm{d}t} = kP(M-P), \tag{3.11} \end{equation}\] subject to \[\begin{equation*} P(t_{0}) = P_{0}, \end{equation*}\] where \(k\) is a positive constant \(k > 0\), and is referred to here as a growth constant.

This model described in Equation (3.11) was first introduced by the Dutch mathematical biologist Pierre-Francois Verhulst (1804–1849), and is referred to as the logistic growth model. Verhulst developed his model in 1838 after having read Mathus’ essay, and extended this for populations with resource limitations. The logistic model is known to agree quite well for populations of organisms that have very simple life histories, for instance yeast growing in a culture where space is limited.

6. Model Solution We can separate the variables and rewrite (3.11) by moving all terms involving \(P\) and \(\textrm{d} P\) to one side of the equation and all terms in \(t\) and \(\textrm{d} t\) to the other. This gives, \[\begin{equation*} \dfrac{ \textrm{d} P}{P(M-P)} = k \textrm{d} t. \end{equation*}\] We use the algebraic concept of partial fraction decomposition to get that \[\begin{equation*} \dfrac{1}{P (M - P)} = \dfrac{1}{M} \left(\dfrac{1}{P} + \dfrac{1}{M - P}\right). \tag{3.12} \end{equation*}\] Thus, (3.12) can be rewritten as \[\begin{equation*} \dfrac{\textrm{d} P}{P} + \dfrac{\textrm{d} P}{M - P} = k M t + c \end{equation*}\] which integrates to \[\begin{equation} \ln{P} - \ln{(M - P)} = k M t + c \tag{3.13} \end{equation}\] for some arbitrary constant \(c\). Using the initial condition, we evaluate \(c\) in the case \(P < M\), \[\begin{equation*} c = \ln{\dfrac{P_{0}}{M - P_{0}}} - k M t_{0}. \end{equation*}\] Substituting into (3.13) and simplifying gives \[\begin{equation*} \ln{\dfrac{P}{M - P}} - \ln{\dfrac{P_{0}}{M - P_{0}}} = k M(t - t_{0}) \end{equation*}\] or \[\begin{equation*} \ln{\dfrac{P (M - P_{0})}{P_{0}(M - P)}} = k M(t - t_{0}). \end{equation*}\] Exponentiating both sides of this equation gives \[\begin{equation*} \dfrac{P (M - P_{0})}{P_{0}(M - P)} = e^{k M (t - t_{0})} \end{equation*}\] or \[\begin{equation*} P_{0} (M - P) e^{k M (t - t_{0})} = P(M - P_{0}). \end{equation*}\] Then, \[\begin{equation*} P_{0} Me^{k M (t - t_{0})} = P(M - P_{0}) + P_{0} P e^{k M (t - t_{0})}, \end{equation*}\] so solving for the population \(P\) gives \[\begin{equation*} P(t) = \dfrac{P_{0} M e^{k M (t - t_{0})}} {M - P_{0} + P_{0} e ^{k M (t - t_{0})}}. \end{equation*}\]

7. Model Interpretation, Verification, and Validity The above logistic model (3.11) can also be solved computationally and the codes and plots are shown below:

The above s-shaped (sigmoid) curve is called a logistic curve.

Thinking Questions:

What do the above graphs tell us?
Why are the two plots vastly different? (Hint: Look at the code for both plots. What is different? What does that tell us?)
What happens to the population as \(t \to \infty\)?
When does the rate of increase of the population reach a maximum according to Model 3.3?
If in 1970 \(P = 4 \times 10^9\), in 1990 \(P = 5 \times 10^9\) and \(M = 12 \times 10^9\), estimate the world population in 2011.

8. Model Refinement, Implementation, Management, and Maintenance

Thinking Question: Can you think of ways in which we could refine Model 3.3?

To estimate \(P\) as \(t \to \infty\), we rewrite this last equation as \[\begin{equation*} P(t) = \frac{M P_{0}}{P_{0} + (M - P_{0}) e^{-k M (t - t_{0})}}. \end{equation*}\] We can simplify this as follows. Define \[\begin{equation*} k = \left(1 - \frac{M}{P_{0}} \right), \end{equation*}\] then \[\begin{equation} P(t) = \frac{M}{ 1 - k e^{-k M (t - t_{0})}}. \tag{3.14} \end{equation}\] This can be rewritten as either \[\begin{equation*} P(t) = \frac{P_{0}}{\frac{P_{0}}{M} + \left( 1 - \frac{P_{0}}{M} \right) e^{-k M \left(t - t_{0}\right) } } . \end{equation*}\] or \[\begin{equation*} P(t) = \frac{M}{ 1 - \left(1 - \frac{M}{P_{0}} \right) e^{-k M (t - t_{0})}}. \end{equation*}\]

Notice from Equation (3.14) that \(P(t)\) approaches \(M\) as \(t\) tends to infinity. Moreover, from Equation (3.11) we calculate the second derivative \[\begin{equation*} P'' = k M P' - 2 k P P' = k P' (M - 2 P) \end{equation*}\] so that \(P'' = 0\) when \(P = \frac{M}{2}\). This means that when the population \(P\) reaches half the limiting population \(M\), the growth \(\frac{\textrm{d} P}{\textrm{d}t}\) is the most rapid and then starts to diminish toward zero. One advantage of recognising that the maximum rate of growth occurs at \(P = \frac{M}{2}\) satisfied that the growth involved is essentially logistic, if the point of maximum rate of growth has been reached, then \(\frac{M}{2}\) can be estimated.

3.6 Models involving Decay

In this Section, we consider models involving radioactive substances, and in particular focusing on radioactive decay.

Radioactive substances decay at a rate proportional to their mass. Its mass decays to the environment with time due to forces of radiation that are acting upon the substance.Experiments show that at each instant a radioactive substance decomposes, and is thus decaying in time proportional to the amount of substance present.

Another key concept that arises here deals with the half-life of a radioactive substance. In physics, the half-life is a measure of the stability of a radioactive substance. The half-life is simply the time at which the substance decays to half of its original mass.

Model 1

Consider a radioactive substance \(A\). If initially there is \(M\)g (grams) of \(A\), construct a mathematical model that describes the decay of the substance with time.

Thinking Question: Would the formulation be acceptable as \[\begin{equation*} \dfrac{\textrm{d} A}{\textrm{d}t} = k A, \end{equation*}\] subject to \[\begin{equation*} A(0) = M, \end{equation*}\] where \(k<0\) and \(A \geq 0\)?

Model 2

Suppose that a radioactive substance \(A\) decays into a non-radioactive substance \(B\). If initially there is \(M\)g of A and none of B, construct a mathematical model that describes the amount of \(A\) and \(B\) as a function of time.

Model 3

Suppose that a radioactive substance \(A\) decays into another radioactive substance \(B\) which in turn decays into a non-radioactive substance \(C\). If initially there is \(M\)g of \(A\), none of \(B\) and none of \(C\), construct a mathematical model that describes the amount of \(A\), \(B\) and \(C\) as a function of time.

Model 4

Suppose that a radioactive substance \(A\) decays into another radioactive substance \(B\) which in turn decays into a non-radioactive substance \(C\). If initially there is none of \(A\), \(B\) or \(C\), and if substance \(A\) is then supplied at a constant rate to the reactor, construct a mathematical model that describes the amount of \(A\), \(B\) and \(C\) as a function of time.

Exercise:

Suppose that the rate of growth of the population in S.A. is proportional to the number of people living at any given time. If in 1970 it was estimated that there were 15 million people living in S.A., and in 1980 it was estimated that this number had increased to 20 million, estimate the population of S.A. in the year 2003.
Let \(n = n(t)\) be the size of a population of a certain country at any time \(t\), \(- \infty < t < \infty\). Suppose that the maximum population size that the country can possibly sustain is \(N\). Suppose further that the rate of growth of the population at any current time \(t\) is proportional to both the current population size and the difference between the maximum population size and its current size (constant of proportionality \(\lambda > 0\)).
- 1. If at \(t = 0\), \(n = N_0\), derive a mathematical expression for \(n\) in terms of \(N_0\), \(\lambda\), and \(t\).
- 1. Sketch, by inspection, the graph of this function.
- 1. When is the rate at which the population is increasing a maximum?
In a particular country the population is expanding at a rate which is directly proportional to the population size \(P\). There is also a net outflow of people from the country (more people are emigrating than there are immigrating) at a constant rate \(\alpha\).
- 1. If \(t\) is the time, and the population size is \(P_0\) when \(t = 0\), derive an expression for the population size \(P\) as a function of the time \(t\).
- 1. Sketch, by inspection, the graph of \(P = P(t)\).
The growth rate of bacteria in a culture medium is directly proportional to the difference between the number of bacteria and a certain optimal number \(\bar N\).
- 1. Derive an expression for the number of bacteria \(n\) as a function of the time \(t\) given that the initial number of bacteria placed in the culture medium is \(N_0\) and that the constant of proportionality is \(\lambda\).
- 1. Sketch, by inspection, the graph of \(n = n(t)\).
- 1. How long does it take for the difference in the number of bacteria and the optimal number to reduce to \(1/4\) of the initial difference?
The temperature \(T\) of a body will increase or decrease at a rate proportional to the temperature difference respectively below or above the surrounding temperature, \(\bar T\), the constant of proportionality being \(k\).
- 1. Derive an expression depicting the temperature of the body as a function of the time given that its initial temperature is \(T_0\).
- 1. Sketch, by inspection, the graph of \(T = T(t)\) when \(T_0 < \bar T\), and when \(T_0 > \bar T\).
Consider a cell suspended in a fluid containing a particular solute. If initially the concentration of this solute within the cell is less than that in the surrounding fluid then solute will flow into the cell through its permeable cell wall at a rate greater than at which solute will flow out of the cell, resulting in a net flow of solute into the cell. Conversely, if initially the concentration of solute within the cell is greater than that in the surrounding fluid, there will be a net flow of solute out of the cell. Fick’s law states that if the surface area of the cell is assumed to remain constant then the rate at which the concentration of solute inside the cell increases or decreases is directly proportional to the difference in concentrations of the solute inside and outside the cell.
- 1. If the concentration of solute within the cell is denoted by \(c = c(t)\) where \(t\) is the time, the concentration of solute in the surrounding fluid is maintained at a constant value \(\alpha\), and the constant of proportionality is denoted by \(k\), express Fick’s law mathematically in the form of a simple differential equation.
- 1. Solve this equation given that \(c(0) = c_0\).
- 1. Sketch, by inspection, the graph of \(c = c(t)\) where \(c_0 < \alpha\), and when \(c_0 > \alpha\).
Suppose that \(x_0\) is the number of antelope in a certain game park at a time \(t = 0\) and that \(x = x(t)\) is the number of antelope at any subsequent time \(t \geq 0\).
- 1. If the approximate number of antelope at any time \(t\) can be described by the differential equation \[\begin{equation*} \dfrac{\textrm{d} x}{\textrm{d}t}= kx \cos t, \quad t \geq 0, \end{equation*}\] where \(k\) is a constant of proportionality, express the approximate antelope population size \(x\) in terms of \(x_0\), \(k\), and \(t\).
- 1. Sketch, by inspection, the graph of \(x\) against \(t\), \(t \geq 0\).
Consider the following situation: A given quantity of a particular drug is taken orally. The drug passes from the stomach into the bloodstream. The drug is then gradually eliminated from the bloodstream by the kidneys. Suppose that the rate at which the drug passes from the stomach to the bloodstream is proportional to the amount of drug present in the stomach (constant of proportionality \(\alpha\)), and that the rate at which the drug is eliminated from the bloodstream is proportional to the amount of drug present in the bloodstream (constant of proportionality \(\beta\)).
- 1. If initially (at \(t = 0\)) the amount of drug taken is \(M\), derive expressions which respectively give the amount of drug present in the stomach and the bloodstream as functions of the time \(t\), \(t \geq 0\) (i) for \(\alpha \neq \beta\), and (ii) for \(\alpha = \beta\).
- 1. When, for each case, will the amount of drug in the bloodstream reach a maximum?
- 1. Sketch, by inspection, the corresponding graphs.
Referring to the previous problem, suppose that, as the patient takes the drug orally, they are also placed onto an intravenous drip which supplies the same drug to the bloodstream at a constant rate \(k\).
- 1. Derive an expression for the amount of drug present in the patient’s bloodstream as a function of time. Assume \(\alpha \neq \beta\).
- 1. Sketch, by inspection, the corresponding graphs.
Let \(x = x(t)\) and \(y = y(t)\) denote respective deviations from normal levels of glucose and insulin in the bloodstream at any time \(t\). Consider the situation in which the glucose level and/or the insulin level have been disturbed in some way, for example by eating glucose. Suppose that any positive deviations in the levels of either glucose or insulin will cause the body to eliminate glucose from the bloodstream, whereas any negative deviations in these levels will cause the body to manufacture more glucose. Furthermore a positive deviation in the insulin level also causes the body to eliminate insulin from the bloodstream and conversely a negative deviation in the insulin level causes the body to manufacture more insulin. However, a positive deviation in the glucose level increases the manufacture of insulin and conversely a negative deviation in the glucose level causes the body to eliminate insulin. If the rates of change of the levels are related to the magnitude of the deviations from normal levels, suggest possible mathematical formulations of the physical situation. Consider the following (very idealized) formulation of the problem: \[\begin{align*} \dfrac{\textrm{d} x}{\textrm{d}t} &= -kx-ky,\\ \dfrac{\textrm{d} y}{\textrm{d}t} &= kx-ky. \end{align*}\]
- 1. If initially a small amount of glucose was injected into the bloodstream thus immediately raising the glucose level by an amount \(x_0\) above the normal level, describe the subsequent behaviour of glucose and insulin in the bloodstream mathematically.
- 1. Sketch, by inspection, the corresponding graphs.

Selected Answers:

\(38,76\) million
- 1. \(n=\dfrac{N}{1+\left(\frac{N}{N_0}-1\right)e^{-N\lambda t}}\)
- 1. \(t=\frac{1}{N\lambda} \ln \left(\frac{N}{N_0}-1\right)\)
- 1. \(P=\left(P_0-\frac{\alpha}{k}\right)e^{k t}+\frac{\alpha}{k}\)
- 1. \(n= \bar{N}-(\bar{N}-N_0)e^{-\lambda t}\)
- 1. \(t=\lambda^{-1} \ln 4\)
- 1. \(T= \bar{T}-(\bar{T}-T_0)e^{-k t}\)
- 1. \(c =\alpha−(\alpha−c_0)e^{-k t}\)
\(x=x_0e^{k\sin t}\)
- 1. 1. \(S(t)=Me^{-\alpha t}\), \(B(t)=\frac{\alpha M}{\alpha-\beta}\left(e^{-\beta t}-e^{-\alpha t}\right)\)
    2. \(S(t)=Me^{-\alpha t}\), \(B(t)=\alpha M t e^{-\alpha t}\)
- 1. 1. \(\frac{1}{\alpha-\beta} \ln \left(\frac{\alpha}{\beta}\right)\)
    2. \(\frac{1}{\alpha}\)
- 1. \(B(t)=\frac{\alpha M}{\beta-\alpha}e^{-\alpha t}-\left(\frac{\alpha M}{\beta-\alpha}+\frac{k}{\beta}\right)e^{-\beta t}+\frac{k}{\beta}\)

Did you get it?

Check your understanding of some of the concepts covered at this stage by attempting the DYGIT? on Growth and Decay Models. This is a formative assessment task and does not count for marks so please do it on your own to ascertain your own learning.

In the next section, we consider another important model of continuous change from Physics.

3.7 Newton’s Law of Cooling/Warming

Some physical systems have the interesting behaviour where by the rate of change of some part of that system is proportional to the difference between some initial value and the current value. An example of such a system is the familiar problem of the rate at which something cools by losing heat to its environment. This feature of heat moving from a hot body to a cooler one can be seen in the melting of ice, the radiance of the sun and, for a problem that is closer to home, the cooling of tea at teatime. The following example discusses a solution to this problem that was first developed by Isaac Newton.

Newton’s Law of Cooling/Warming is a fundamental concept in the study of heat transfer and mathematical modeling. It describes how the temperature of an object changes concerning its surroundings. This law is especially significant in fields such as physics, engineering, and environmental science. In this Section, we will explore the principles of Newton’s Law of Cooling/Warming, understand its mathematical formulation, and solve various problems to gain insights into its applications.

Newton’s Law of Cooling/Warming finds applications in various real-life scenarios, such as weather forecasting, cooking, and thermal engineering. Understanding the principles behind this law enables us to predict and control temperature changes in practical situations.

Formulation of Newton’s Law of Cooling/Warming

Example 3.4 (Cooling a Cup of Tea) Consider the situation of a cup of hot tea on a table in a room at room temperature. How would we model the cooling of the tea?

The rate of change of the temperature of an object is proportional to that of the temperature of the medium surrounding that object. Two varying values are said to be proportional to one another if they are related by a multiplicative constant, this is known as the constant of proportionality. That is there is a constant ratio between the two values. Keeping these concepts in mind, we can step through the modelling process.

1. Problem Identification We want to find a function that describes the temperature of the tea for any given time.

2. Assumption Specification There is a distinction that needs to be made between temperature and heat, the two most important physical quantities in this problem.

First, let us assume that the temperature of the object is homogeneous, meaning that it is uniform throughout. In this case, the temperature will be a function of time alone. Temperature is usually measured in degrees Celsius \(^\circ\)C.

Second, consider the quantity heat. The temperature of the object changes due to heat energy being transferred with the surrounding air. Remember that heat is always transferred from a region of high temperature to a region of lower temperature. Since heat is a form of energy, it is measured in Joules. Thus, we need an need an equation that describes the rate of heat transfer to the surroundings.

A mechanism for heat to be lost from an object is that of exchanging heat energy with its surroundings. We therefore assume that the rate of heat flow is directly proportional to the temperature difference between that of the the object and its immediate surroundings.

For the problem under consideration, we thus will assume that

the temperature of the tea \(T\) is a differentiable function of \(t\) and that the temperature of the room is constant, since the surrounding air is of such a large volume that the effect of the temperature of the tea will be negligible.
the rate of change of the temperature of the tea is proportional to the difference in the temperature of the tea and the temperature of the room.

3. Variable Classification Suppose the temperature of the tea was \(T\) at time \(t\), such that \(T(t)\), and the room temperature was \(T_m\).

4. Model Construction Newton’s Law of Cooling/Warming states that the rate at which the temperature of an object changes is directly proportional to the difference between the temperature of the object (\(T\)) and the ambient temperature (\(T_{\text{m}}\)), which is the temperature of the surrounding medium.

Newton’s law of cooling/warming can be translated into the mathematical statement:

\[\begin{equation*} \text{Rate of change of heat content} \propto \text{rate heat exchanged with surroundings}, \end{equation*}\] or \[\begin{equation*} \dfrac{dT}{dt} \propto \pm (T - T_{\text{m}}). \end{equation*}\]

The correct sign for the temperature difference is determined in any specific problem by the direction of heat transfer and whether the object is gaining or losing heat. Mathematically, it can be expressed as an equation by introducing a constant of proportionality \(k\):

\[ \dfrac{dT}{dt} = k(T - T_{\text{m}}), \]

where:

\(\frac{dT}{dt}\) represents the rate at which the temperature of the object changes with respect to time (\(t\)),
\(T(t)\) represents the temperature of the obect at time \(t\),
\(T_{\text{m}}\) is the ambient temperature - temperature of the surrounding medium/environment, and
\(k\) is the cooling or warming constant specific to the object and the medium.

5. Model Problematization The constant \(k\) is vital in understanding the behaviour of the system. For either case, cooling or warming, if \(T_{\text{m}}\) is a constant, it stands to reason that the constant of proportionality \(k<0\). You can check this by problematizing each model formulation for warming and cooling.

For cooling, the object cools down to the ambient temperature. For warming, the object warms up to the ambient temperature. Thus the mathematical formulation for Newton’s law of cooling/warming can be described by the linear first-order differential equation:

\[ \dfrac{dT}{dt} = k(T - T_{\text{m}}), \]

where \(T_{\text{m}}\) is a constant and \(k<0\).

Note that in the preceding models, we have assumed \(k<0\) to be a constant. However, this is a limitation of the model as the rate of heat lost from a surface will be affected by the air flow near it.

For this particular problem, since we want the temperature to go down when the tea is warmer than its surrounding environment we will assign a negative value to the coefficient, i.e.

\[\begin{equation} \dfrac{dT}{dt} = -k(T - T_{\text{m}}), \tag{3.15} \end{equation}\] where \(T_{\text{m}}\) is a constant and \(k<0\).

6. Model Solution Solving problems related to Newton’s Law of Cooling/Warming involves solving first-order ordinary differential equations. Techniques like separation of variables and integrating factors are commonly employed.

We can solve this model by separating variables and integrating Equation (3.15) to yield

\[\begin{equation} T(t) = T_m + C e^{-kt}, \tag{3.16} \end{equation}\] where \(C\) is a constant of integration that is determined by some collection of conditions specified by the initial state of the system.

7. Model Interpretation, Verification, and Validity Several examples of Equation (3.16) are plotted below. The cooling curves are shown for a collection of systems for differing values of the cooling coefficient \(k\).

Interpretation

When \(T < T_m\), the gradient is negative, and when \(T_m < T\) the gradient is positive. These both make sense since we would expect the tea to warm up if the room temperature is higher than its temperature and to cool down when the room temperature is lower than its temperature.
When \(T_m = T\) we have reached an equilibrium point since the rate of change is \(0\).

8. Model Refinement, Implementation, Management, and Maintenance

Limitations and Considerations

While Newton’s Law of Cooling/Warming provides valuable insights, it assumes certain ideal conditions, such as constant cooling/warming rates and uniform temperature distribution. In real-world scenarios, factors like air circulation, radiation, and material properties might influence the accuracy of predictions. It is essential to be aware of these limitations when applying the law to practical situations.

We will now consider a common model that arises in a first-course in Economics.

3.8 Continuous Supply and Demand

Example 3.5 (Continuous Supply and Demand) Consider an economy in which manufacturers control production to meet demand, while retailers control demand to meet the supply. What might be the supply and demand on retailers at some time \(t\)?

1. Problem Identification We are interested in finding equations that describe the changes in demand and supply for retailers in an economy for any given point in time.

2. Assumption Specification

Since the retailers want to serve the demand by the customers, and their ability to do so is limited by their ability to produce goods, we should expect that there is some relation between the production \(P\) and the demand \(D\).
Clearly, it is not economical to produce more than can be sold.
Assume that at any time \(t\) the rate of production of some commodity is proportional to the difference in production and demand, and the rate of consumption is proportional to the difference in demand and production.

3. Variable Classification Suppose at time \(t\) the manufacturer production is \(P\) and retailer demand is \(D\).

We want to find the \(P(t)\) and \(D(t)\), the supply and demand functions, respectively.

4. Model Construction Suppose that at time \(P(t = 0) = P_{0}\) and \(D(t = 0) = D_{0}\).

A suitable continuous model for this coupled system is

\[\begin{equation*} \dfrac{dP}{dt} = \alpha (D - P) \qquad \text{and} \qquad \dfrac{dD}{dt} = \beta (P - D). \end{equation*}\]

Note the symmetry of this system under transposition of \(P\) and \(D\), and \(\alpha\) and \(\beta\).

5. Model Problematization Go through this procedure on your own.

6. Model Solution Consider first the continuous model, more conveniently rewritten as \[\begin{equation*} P' = \alpha (D - P) \qquad \text{and} \qquad D' = \beta (P - D), \end{equation*}\] which implies, \[\begin{equation*} \beta P = D' + \beta D \qquad \text{and} \qquad \alpha D = P' + \alpha P, \end{equation*}\] and \[\begin{equation*} \beta P' = D'' + \beta D' \qquad \text{and} \qquad \alpha D' = P'' + \alpha P'. \end{equation*}\] From these equations we note that, \[\begin{align*} \alpha \beta P &= \alpha D' + \alpha \beta D = (P'' + \alpha P') + \beta(P' + \alpha P), \\ \alpha \beta D &= \beta P' + \alpha \beta P = (D'' + \beta D') + \alpha(D' + \beta D). \end{align*}\] or, \[\begin{equation*} P'' + (\alpha + \beta) P' = 0 \qquad \text{and} \qquad D'' + (\alpha + \beta) D' = 0. \end{equation*}\] Define, \(\gamma = \alpha + \beta\), then, \[\begin{align*} P'' + \gamma P' = 0 \qquad \text{and} \qquad D'' + \gamma D' = 0. \end{align*}\]

Assuming trial solutions \(P(t) = a e^{\lambda t}\) and \(D(t) = a e^{\lambda t}\) yield, in each case, \(\lambda = 0\), or \(\lambda = - \gamma\), and subsequent solutions, \[\begin{equation*} P(t) = a + b e^{ - \gamma t} \qquad \text{and} \qquad D(t) = c + d e^{ - \gamma t}, \end{equation*}\] and so, \[\begin{align*} P' = - \gamma b e^{ - \gamma t} = \alpha (c - a) + \alpha (d - b) e^{- \gamma t}, \\ D' = - \gamma d e^{ - \gamma t} = \beta (a - c) + \beta (b - d) e^{- \gamma t}. \end{align*}\] Solving for \(a, b, c\) and \(d\) yields, \[\begin{equation*} a = c = \frac{\alpha D_{0} + \beta P_{0}}{\gamma}, \qquad b = \frac{\alpha P_{0} - \alpha D_{0}}{\gamma} \qquad \text{and} \qquad d = \frac{\beta D_{0} - \beta P_{0}}{\gamma}, \end{equation*}\] to give, \[\begin{align*} P(t) &= \frac{\alpha D_{0} + \beta P_{0}}{\gamma} + \frac{\alpha P_{0} - \alpha D_{0}}{\gamma} e^{ - \gamma t}, \\ D(t) &= \frac{\alpha D_{0} + \beta P_{0}}{\gamma} + \frac{ \beta D_{0} - \beta P_{0}}{\gamma} e^{ - \gamma t}. \end{align*}\]

Note, again, the symmetry of each model of this system under transposition of \(P\) and \(D\), and \(\alpha\) and \(\beta\).

7. Model Interpretation, Verification, and Validity

For the purpose of comparison, suppose \(\alpha = \beta = k\), then \(\gamma = 2 k\). Then the continuous model becomes \[\begin{align*} P(t) &= \frac{1}{2} \left( D_{0} + P_{0} \right) + \frac{1}{2} \left(P_{0} - D_{0} \right) e^{ - 2 k t}, \\ D(t) &= \frac{1}{2} \left( D_{0} + P_{0} \right) + \frac{1}{2} \left(D_{0} - P_{0} \right) e^{ - 2 k t}. \end{align*}\]

The value of \(k\) in each exponential term determines the behaviour of each model. The continuous models have a single critical \(k\) value, namely \(k = 0\) that splits the behaviour of the continuous model according to \(k < 0\), \(k = 0\) and \(k > 0\). These conditions on the \(k\) split the relative behaviour of the discrete model and continuous model into the following five cases.

\(k = 0\) - The continuous models give solutions that are identical to the discrete models.
\(0 < k < \frac{1}{2}\) - The continuous and discrete models are qualitatively the same, and decay exponentially to a constant value \(\frac{1}{2} \left( D_{0} + P_{0} \right)\), although the actual values given by each model may differ.
\(k =\frac{1}{2}\) - The discrete models are constant, while the continuous model solutions tend to the discrete model solutions after sufficiently large parameter values \(t\).
\(\frac{1}{2} < k < 1\) - The discrete models oscillate with amplitude that decay exponentially about a constant value where as the continuous models are purely decaying and tend to the same constant value.
\(k = 1\) - The discrete models oscillate indefinitely with fixed amplitude, while the continuous models decay exponentially and tend to a constant value.
\(k > 1\) - The discrete models oscillate indefinitely with increasing amplitude, while the continuous models decay exponentially and tend to a constant value. In this case the discrete model is unstable.

The relative behaviours of this model at the critical values of \(k\) and at the non-critical values of \(k\) are shown in the figures below.

This plot shows the behaviour of \(P\) (solid) and \(D\) (dotted) at critical points \(k = 0\) (triangle), \(k = \frac{1}{2}\) (square) and \(k = 1\) (diamond).}

This plot shows the behaviour of \(P\) (solid) and \(D\) (dotted) between critical points \(0 < k < \frac{1}{2}\) (triangle), \(\frac{1}{2} < k < 1\) (square) and \(1 < k\) (diamond).}

Exercise:

When a cake is removed from an oven, its temperature is measured at \(150^\circ\)C. Three minutes later its temperature is \(90^\circ\)C. How long will it take for the cake to cool off to a room temperature of \(20^\circ\)C?
In cooking, understanding the cooling/warming rates of different foods is crucial. Consider a dish taken out of an oven with an initial temperature of \(T_0 = 180^\circ\)C. Using the cooling constant \(k = - 0.03\), calculate the time it takes for the dish to cool down to a safe eating temperature of \(T_{\text{m}} = 60^\circ\)C.