Chapter 3 Arrays & Vectors

3.1 Abstract Data Type: Lists

Suppose you want to sort a list of numbers…
Suppose you want to print a list of student grades…
Suppose you want to store a list of dank memes…

In many problems, we need to keep or manipulate a list of some type of object. In the examples above these objects are numbers, grades, and memes, but regardless of the object that we are storing, the operations that we would perform on the list are usually the same:

Add an object to the list (at the front, at the back, or before index i)
Remove an object from the list (at the front, at the back, or at index i)
Get an object from the list (at the front, at the back, or at index i)
Get the size of the list

When we think of a list in this way, we are specifying what we would like to do with a list (i.e. the interface or declaration) but not how the list itself is represented in memory (i.e. the implementation or definition). When we define the interface in this way, we are defining an Abstract Data Type and in this case, the ADT is a list.

In future, when we’re working on our algorithms, we can just use a list to store all our objects and we don’t need to think about how the list was implemented, only what we want to do with the list. This abstraction allows us to think about our problem at a high level, without having to think about the details of memory management, efficiency, correctness etc.

But someone has to think about these things at some point to code them into the language. It’s also important that if you are going to use these structures in your code that you know when they are good or bad. This is important because:

for(int i = 0; i < n; ++i){
  myList.push_back(i);
}

will do a linear amount of work – $O(n)$ – if push_back is constant, but it will do a quadratic amount of work – $O(n^2)$ – if push_back is linear.²

Unfortunately, there is no free lunch. Being fast at one operation often means a trade-off in the speed of another or even increasing the memory requirements. We will see this happen many times and often we have to choose the data structure that is optimal for the operation that happens most often. For example, if we create the list once, but then search it many times we probably care more about the get operations over the push_back operations. If we are only ever adding and removing at the back of the list, then it is important the push_back and pop_back are fast, but get(index) doesn’t matter at all.

In the long run, knowing the pros and cons of various data structures allows you to select the correct implementation to ensure your algorithms run efficiently.

Our first implementation of a list will be using blocks of contiguous memory called arrays, but before we talk about our first list implementation, let’s discuss memory management.

3.2 Memory Management

Remember

There are two spaces where we can allocate memory: The stack and the heap.
Automatic variables are allocated on the stack.
Dynamic memory is allocated on the heap.
Frames are like Pancakes: You add to the top of the stack, you remove from the top of the stack.
The call stack holds a frame for every function that gets called. The frame contains space for all the automatic variables inside the function.
When the function finishes, the frame gets popped off of the call stack. We always remove from the top of the stack. All the automatic variables are automatically destroyed.
Dynamically allocated memory is controlled by us and we are in charge of returning it to the operating system when we’re finished.
Dangling points point to memory that we no longer own. Don’t dereference them!
Allocate with square brackets (p = new int[42]) $\rightarrow$ delete with square brackets (delete [] p)
Allocate without square brackets (p = new int) $\rightarrow$ delete without square brackets (delete p)
If we forget to return dynamically allocated memory to the operating system (delete or delete[]) then we have a memory leak.

3.3 Contiguous Memory & Pointer Arithmetic

One thing that makes arrays appealing is that they are extremely fast to access, no matter how many items are stored in it. This because all the items are stored contiguously. This means that all the blocks of memory are allocated consecutively – directly next to each other. When we allocate space for $n$ items, we allocate one large block of $n*\mathrm{datatype~size}$ bytes. In fact, in the C programming language you have to calculate the number of bytes yourself and then cast to the correct type. The C++ approach is much safer.

// Automatic Variables - C and C++
// Note that the size cannot be a variable, it must be a number known at compile-time.
int myList[42]; 

// Dynamic Allocation
int* myListC   = (int*) malloc(n*sizeof(int)); // C [Not typesafe]
int* myListCpp = new int[n]; // C++

Figure 3.1 shows the myList pointer which contains the address of the first object stored in the array. In this case, the first object is stored at 0x04 and each integer takes up 32 bits (4 bytes).

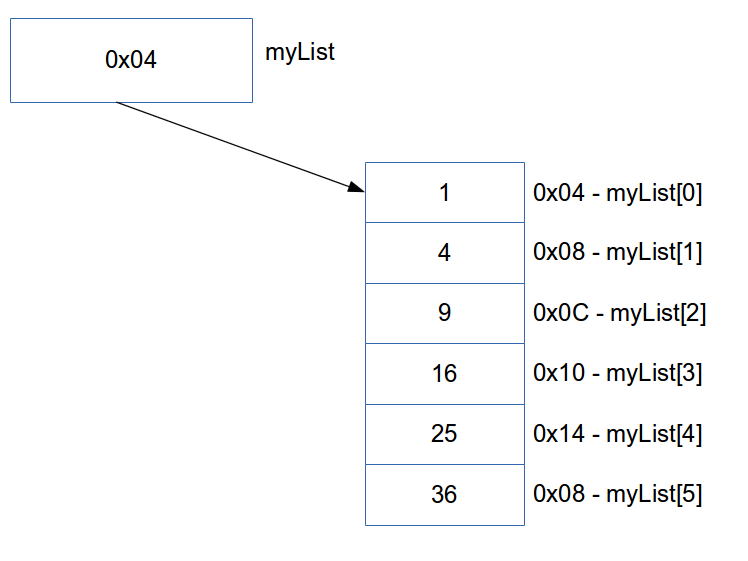
Figure 3.1: Memory Layout of an Array

Because every object/block in the memory is the same size, we can calculate the address of an item at index $i$ by taking the address of the first item in the array and adding $i*\mathrm{datatype~size}$ to it. For example, to get the address of myList[4] we would say myList + i*sizeof(int). However, as the compiler knows what type of pointer we are dealing with, it already knows to multiply the index by the size of the data type. It does this automatically, so we rather just say myList + i and the compiler will do the extra work for us. To get the value we simply dereference this new pointer.

This process is called pointer arithmetic.

Index	Object	Value
0	myList[0]	*(myList+0)
1	myList[1]	*(myList+1)
2	myList[2]	*(myList+2)
3	myList[3]	*(myList+3)
4	myList[4]	*(myList+4)
…	…	…
i	myList[i]	*(myList+i)

We can also use pointer arithmetic with a 2D array:

int **myList = new int*[n];
for(int i = 0; i < n; ++i){
  myList[i] = new int[m];
}

// These two lines are the same:
myList[i][j] = 42;
*(*(myList+i)+j) = 42;

Notice that to calculate the address of an object in a 1D array it is one multiplication, an addition and one pointer deference. Regardless of how many items there are in the array ($n$), it will always take the same amount of time to fetch the object. This means that we can access an item in an array in constant time – $O(1)$.

3.4 Increasing the size of an array

As arrays require all memory to be contiguous (otherwise we would not be able to do pointer arithmetic), it means that all the memory needs to be allocated at the start when the array is created – if we allocated the memory in multiple stages, then we’d have no guarantee that each allocation would be next to the previous. Once the block of memory has been allocated, the operating system might allocate other variables in the space neighbouring the current block. Unfortunately, this means that once the block has been allocated, we cannot expand the size of that block because we can’t be sure that the memory adjacent to it is free.

If after the allocation, we later decided that the array isn’t big enough, we would need to make a new, bigger array, and then copy all the items that need across into the new buffer. Finally, we would free the old block of memory because it is no longer needed. For example, we might use the following code.

void reallocate(size_t new_size){
  int* new_buffer = new int[new_size]; // Allocate a new, bigger array
  for(int i = 0; i < n_items; ++i){
    new_buffer[i] = data[i];           // Copy all the old items into the new buffer
  }
  delete [] data;                      // Delete the old buffer
  data = new_buffer;                   // Make the data buffer point to the new memory
  n_allocated = new_size;              // Remember the size of the new buffer
}

Here are some examples of how to increase the size of an array and how to analyse the amount of time taken to do so.

You’ll notice in the code and examples above that all the memory used is dynamically allocated – we always used the new keyword. Unfortunately, when you call a function, the stack frame size for that function’s automatic memory needs to be known upfront. This means that it is impossible to resize an array that allocated on the call stack – doing so would require that we resize the stack frame for the function. The compiler needs to know the size of these frames at compile-time. So when working with arrays allocated on the stack, you are stuck with the size that was used when the code was compiled.³

Similarly, there is no way to manually free memory that was allocated on the stack, and the runtime system will only reclaim that memory once the function is finished.

3.5 `std::array` and `std::vector`

In the C++ Standard Template Library (STL) there are two implementations of array types: std::array and std::vector, which represent arrays with automatic (stack) and dynamic (heap) memory allocation respectively. These classes encapsulate the ideas that we’ve spoken about above and provide you with several convenient functions to help you write your code. You can trust that these classes are implemented correctly and efficiently, which can save you a lot of debugging compared to writing your own versions.

Both of these classes provide size to fetch the number of items, operator[](i) to fetch the value stored at index i without bounds checking, at(i) to fetch the value stored at index i with bounds checking and many other functions. Both containers use contiguous memory and pointer arithmetic for their underlying storage.

Because std::array allocates its memory on the stack, you need to know the size at compile-time. On the other hand, std::vector represents a dynamically allocated array where the storage is on the heap. This means that it can reallocate, expanding or shrinking its memory as necessary. A vector<int> would look similar to the following declaration:⁴

class vector{
  int* data;          // Pointer to storage buffer
  size_t n_items;     // Number of items stored
  size_t n_allocated; // Amount of memory allocated
}

We can then use the following code:

void fun(){
  vector<int> v;
  for(int i = 0; i < 5; ++i){
    v.push_back(i);
  }
  // ...
}

The resulting memory layout would be as shown in 3.2. Note that the vector’s member variables (data, n_items, n_allocated) are allocated on the stack, but the actual storage is dynamically allocated on the heap.

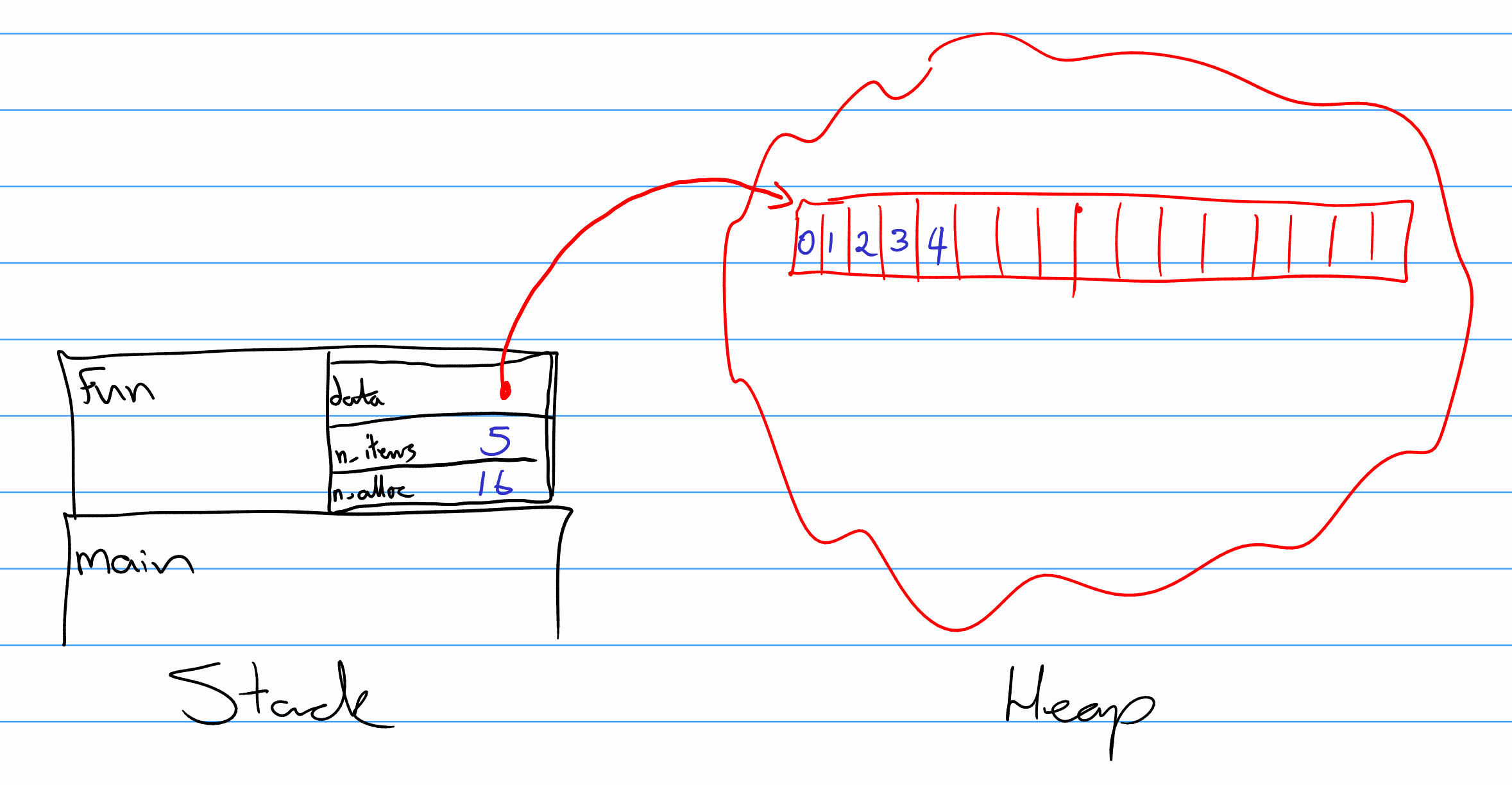
Figure 3.2: Memory Layout of a Vector

In contrast an std::array<int, 5> would have the layout shown in @ref{fig:arrlayout}. Note that the storage is allocated on the stack itself and the class does not need to store the number of items or the size of the current allocation because those cannot change during the objects lifetime.

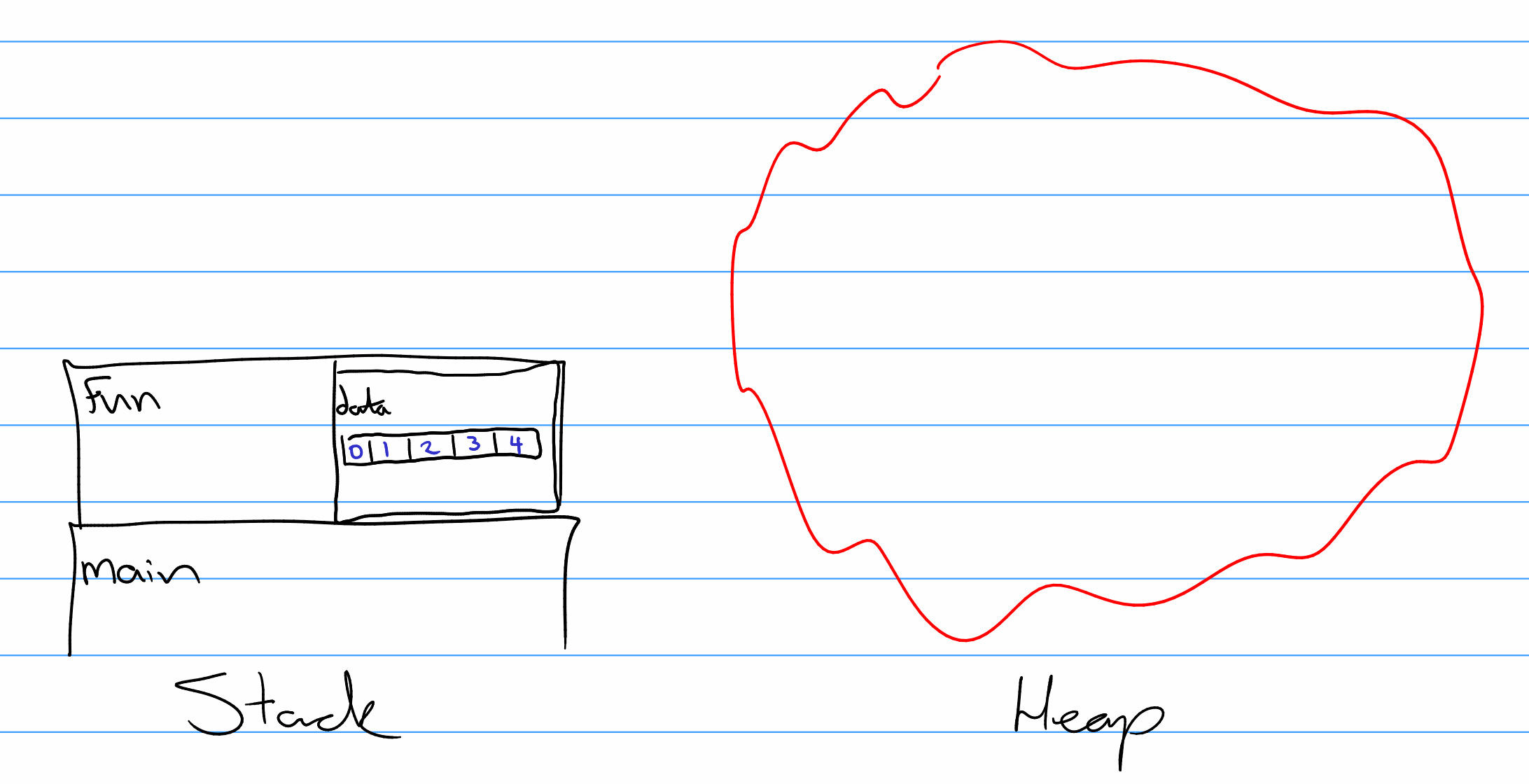
Figure 3.3: Memory Layout of a Vector

3.6 Reallocation & Complexity

The vector class manages 3 main variables: the number of items in the array, the amount of space allocated, and a pointer to the allocated space. The vector maintains storage space that is slightly larger than necessary. When the user tries to add to the back of the array using the push_back function, the vector will first check whether there is any free space – if there is space then the item is simply inserted into the next available block, if not the vector allocates twice as much space as before, copies all the current items into the new space, and then frees the old memory buffer. This strategy finds a good balance between keeping space available for items to be added (thus minimising reallocations and copies) and keeping too much unused space which wastes resources that other programs may need.

Conversely, when removing an item from the back of the list we want to make sure that we give memory back to the operating system when it is no longer necessary. We don’t want to reallocate and copy every time an item is removed – as that would be slow. A naïve approach would be to reallocate every time the vector is half empty but this creates a problem when the user adds and removes items repeatedly as illustrated below.

n_items: 5, n_allocated: 8
pop… n_items: 4, half empty, reallocate
n_items: 4, n_allocated: 4
push… n_items: 5, storage is full, reallocate
n_items: 5, n_allocated: 8
pop… n_items: 4, half empty, reallocate
n_items: 4, n_allocated: 4
push… n_items: 5, storage is full, reallocate
n_items: 5, n_allocated: 8

This causes a large number of unnecessary reallocations – which are slow. The better strategy is to reallocate with twice the space when the vector is full, and then to half the amount of allocated space when the vector is less than a quarter full. This strikes a balance where the vector does not waste too much space when removing items but does not reallocate and copy too quickly,⁵.

Accessing items or indexing into the vector using the operator[] or the at() functions simply uses pointer arithmetic in the background, this means that these functions take constant time – $O(1)$.

Getting the size (number of items in the vector) or the capacity of the allocated storage involves simply returning those values, which are stored inside the class – $O(1)$.

Pushing a new item to the back of the vector has two cases. In the best case, there is already space available to perform the insert and the value is just copied into the memory buffer. This takes constant time – $O(1)$. In the worst case, there is no extra space in the buffer and the vector needs to reallocate memory, copy all the items across, and then free the old memory. In this case, we have $n$ items and each item gets copied once. Therefore we do $O(n)$ operations.

Similarly, when popping from the back of the vector we have two cases again. In the best case, we aren’t wasting too much space and so we don’t have to reallocate. So the vector simply removes the item from the buffer in constant time – $O(1)$.⁶ In the worst case, we decide that we are starting to waste too much memory and we reallocate, which makes $n$ copies again taking us linear time – $O(n)$.

These worst cases seem bad, but by choosing those reallocation thresholds very carefully, we can mathematically prove that over $n$ insertions and/or deletions we still only do a linear amount of work. This is called Amortised Analysis and we say that these functions take Amortised Constant Time. You will learn to do this type of analysis in fourth-year and it shows that even with reallocations, the vector is very efficient.

Another operation that we might care about is inserting or removing at the front of the vector. Unfortunately, there is no way to do this in constant time. If there is still open space at the back of the vector, then we can copy each item one block to the right in order to create space at the front. This involves $n$ copies and is therefore linear time. If there is no space at the back of the vector, then we need to reallocate and once again copy all the items across, again resulting in linear time.

Note that the time complexity of C++ STL containers and algorithms is part of the ISO C++ Standard. This means that for a compiler to be standards compliant, its STL implementation needs to be at least as efficient as mentioned by the standard. Have a look at the different functions offered by the std::vector as well as the associate complexity of each. A reference can be found here: http://www.cplusplus.com/reference/vector/vector/.

3.7 Questions

How would you implement a push_front(int value) function for a std::vector?
1. Are there best and worst cases, or does it always have the same asymptotic complexity?
2. What is the complexity?
How would you implement a push_at(int value, int idx) function for a std::vector?
1. Are there best and worst cases, or does it always have the same asymptotic complexity?
2. What is the complexity?
You would like to create a custom vector object. You don’t ever need the push_back function but you do need a push_front function. How would you implement it and what would the complexity be?
What is the purpose of the begin and end functions of the std::vector and std::array?
Why is the return type of vector<int>::operator[] and vector<int>::at an int& rather than an int?
What does the reserve function do?
What does the resize function do?
When would you prefer an std::array over a std::vector?
Exactly how many items are in the vector after the following code completes? [Try to do this without running the code.]
```
vector<int> v;
for(int i = 0; i < n; ++i){
  v.push_back(i);
}
```
Exactly how many items are in the vector after the following code completes? [Try to do this without running the code.]
```
vector<int> v;
for(int i = 0; i < n*n; ++i){
  v.push_back(i);
}
```

Exactly how many items are in the vector after the following code completes? [Try to do this without running the code.]

vector<int> v;
for(int i = 0; i < n; ++i){
   for(int j = 0; j < n; ++j){
     v.push_back(i);
   }
}

Exactly how many items are in the vector after the following code completes? [Try to do this without running the code.]

vector<int> v;
for(int i = 0; i < n; ++i){
   for(int j = 0; j < i; ++j){
     v.push_back(i);
   }
}

Exactly how many items are in the vector after the following code completes? [Try to do this without running the code.]

vector<int> v;
int i = n;
while(i > 0){
  v.push_back(i);
  i /= 2;        // Hint: Integer division
}

3.8 Additional Reading

https://www.geeksforgeeks.org/introduction-to-arrays/
https://www.geeksforgeeks.org/arrays-in-c-cpp/
http://www.cplusplus.com/reference/vector/vector/
Chapter 3.1, 3.2, 3.3, 3.4 – Weiss (2014)
More detailed and advanced: Chapters 17, 18 and 19 – Stroustrup (2014)

We do something like $an+b$ steps, $n$ times. We’ll look at this case in more detail later.↩︎
In C++ dynamically sized arrays are not allowed on the stack. However, the g++ compiler actually does allow this by changing the size of the stack frame, but it is not part of the C++ standard and this only works in very specific circumstances. This is a feature of C99 (not C++) called Variable Length Arrays that g++ decided to implement. You should avoid using it because other compilers won’t necessarily support it. Also, the stack is usually not big enough for large arrays and these can cause stack overflows – large arrays should never be allocated on the call stack. Every time I compile your code on Moodle, I explicitly tell g++ to disable the VLA extensions.↩︎
Excluding template declarations↩︎
This strategy is followed by most implementations, although the exact coefficient is implementation-dependent.$↩︎
In a real vector, the STL uses ‘placement new’ to construct objects, so when it manually destructs the objects when necessary. This is the only time you should ever manually call a destructor. This is more sophisticated C++ than we’ll cover in this course, so for our purposes, we’ll consider that the objects are simple and can just be overwritten – like an int.↩︎

Chapter 3 Arrays & Vectors

3.1 Abstract Data Type: Lists

3.2 Memory Management

Remember

3.3 Contiguous Memory & Pointer Arithmetic

3.4 Increasing the size of an array

3.5 std::array and std::vector

3.6 Reallocation & Complexity

3.7 Questions

3.8 Additional Reading

3.5 `std::array` and `std::vector`