Chapter 4 Difference Equations
“If by chance I have omitted anything more or less proper or necessary, I beg forgiveness, since there is no one who is without fault and circumspect in all matters.” ― Leonardo Fibonacci (1170-1250)
4.1 Difference Equations and Ordinary Difference Equations
As we seen in the preceding chapters, differential equations are great for modelling situations involving continuous change. If however the change happens incrementally rather than continuously, then differential equations have their shortcomings. Instead we will use difference equations which are recursively defined sequences that allows us to model discrete change. Examples of situations that involve incremental changes include animal populations that mate once a year, interest that is compound monthly, and in economics and infectious disease modelling.
A difference equation is the discrete analogue of a differential equation, and it represents change in the case of discrete intervals. Difference equations are instrumental in modelling such time series because values of these variables can only be measured at discrete intervals, or it is more convenient to do so.
In other words, a difference equation is a mathematical equality that involves the differences between successive values of a function of a discrete variable. A discrete variable is one that is defined only for values that differ by some finite amount, usually a constant and often \(1\). In the next two chapters, our principal object of study is the sequence, that is, a list of numbers of the form \[\begin{equation*} y_0,\:y_1,\:y_2,\:y_3,\dots, \end{equation*}\] which goes on forever. We abbreviate such a sequence as \(y_k\), with the understanding that the index \(k\) takes all non-negative integer values \(0, 1, 2,\dots,\) and so on, and from which the following differences can be found: \[\begin{align*} \Delta y_0 &= y_1-y_0,\\ \Delta y_1 &= y_2-y_1,\\ & \vdots \\ \Delta y_n &= y_{n+1}-y_n. \end{align*}\] We will focus on sequences defined by difference equations, which is also commonly referred to as a recurrence relation.
where \(n\) is the discrete independent variable, and \(y_n\) is the dependent variable that generates the sequence referred to as a recurrence relation. \(n\) is defined in discrete steps and we index across the independent variable \(n\), which has been discretized (made discrete). The collection \(\{(n, y_{n})\}\) is now a discrete, ordered set of points, and \(y\) is a discrete function.
For example:
\[\begin{equation}
x_{n+1}=1.02 x_n; \quad n=0, 1, 2,\dots
\tag{4.1}
\end{equation}\]
The work we do will do regarding difference equations in this course will exclusively involve ordinary difference equations. This means that we will have only one discrete independent variable. For the rest of these notes, any reference to the word difference equation refers exclusively to ordinary difference equations.
Difference equations arise from many sources, and the discrete independent variable \(n\) can signify many different things. We can think of difference equations as illustrating \[\begin{equation*} \text{Future value} = \text{Current value}+\text{Change}. \end{equation*}\] Examples of such equations are:
- Newton’s Method given by the difference equation \[\begin{equation*} x_{n+1}=x_n-\dfrac{f'(x_n)}{f(x_n)}. \end{equation*}\]
- The Fibonacci sequence \(1,\:1,\:2,\:3,\:5,\:8,\:13,\:21,\dots\). This string of numbers referred to as a recurrence relation can be generated from the difference equation \[\begin{equation*} x_{n+1}=x_n+x_{n-1}. \end{equation*}\] Thinking Question: Is this difference equation unique?
- The compound interest formula where interest is earned at distinct points in time (example, compounded monthly), as opposed to continuous compounding: \[\begin{equation*} a_{n+1}=a_n(1+i)^{n}. \end{equation*}\]
4.2 Notation
The notation used in Equation (4.1) will be the convention. From here, it is strongly implicit that \(n\) is an integer value.
4.3 Graphical Representation
The collection of ordered pairs \(\{(n, y_{n})\}\) is a discrete function indexed by the non-negative integers \(n=0, 1, 2,\dots\). It is possible to represent a discrete function graphically as a collection of points \((n, f_{n})\) in the plane, as shown by the examples below:
Examples
Sketch the graphs of the following discrete functions:
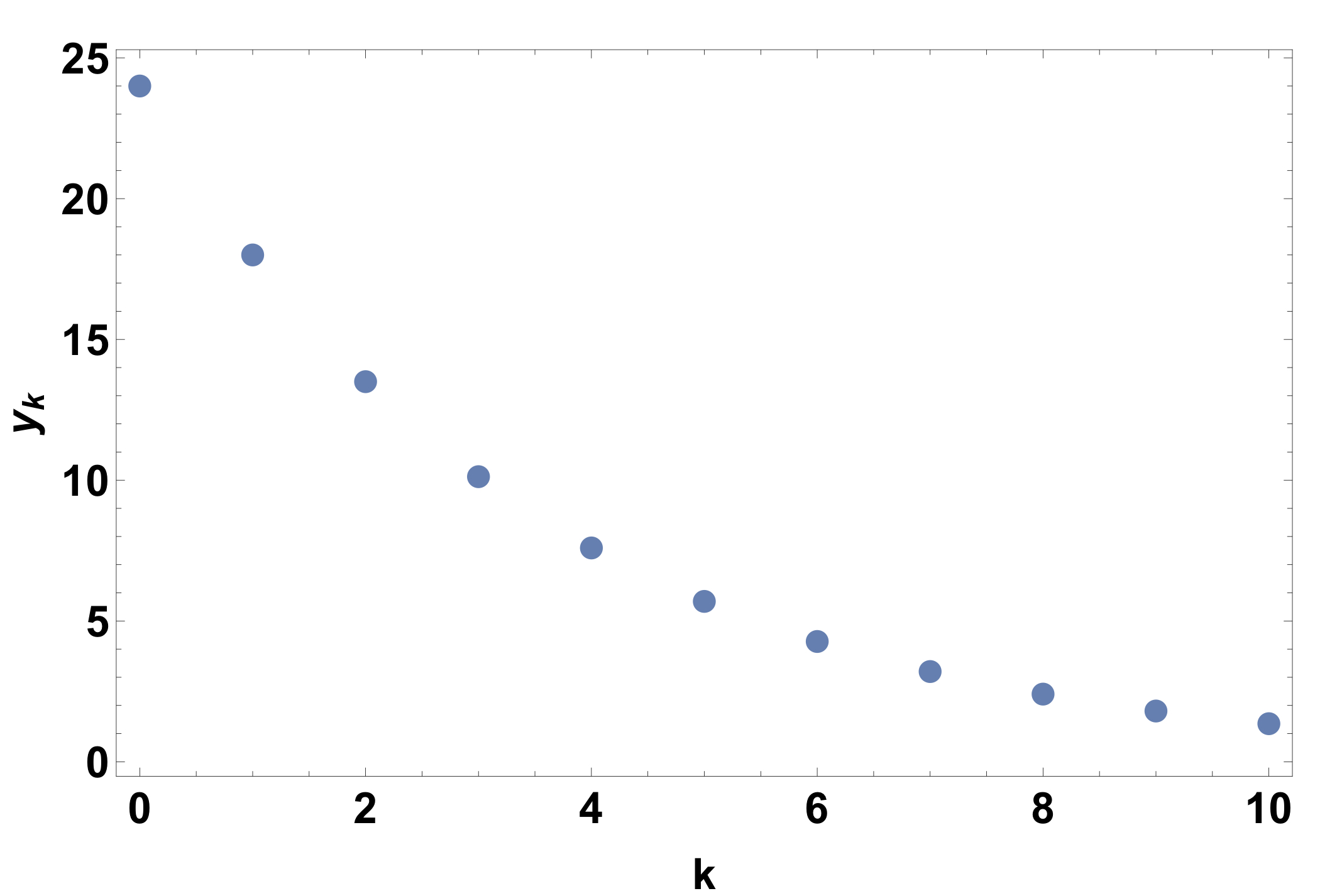
- \(y_k = 24\left(\frac{3}{4}\right)^{k}; \quad k = 0,1,2,\dots\)
We expect this to decay as \(\frac{3}{4} < 1\). So \(\left(\frac{3}{4}\right)^{k}\) will get smaller for increasing powers of \(k\). The recurrence relation can be generated from the above difference equation by indexing across the discrete variable \(k\) to get
\[\begin{align*}
y_0 &= 24\left(\frac{3}{4}\right)^{0}=24,\\
y_1 &= 24\left(\frac{3}{4}\right)^{1}=18,\\
y_2 &= 24\left(\frac{3}{4}\right)^{2}=13.5.\\
& \vdots
\end{align*}\]
This can be graphed to get
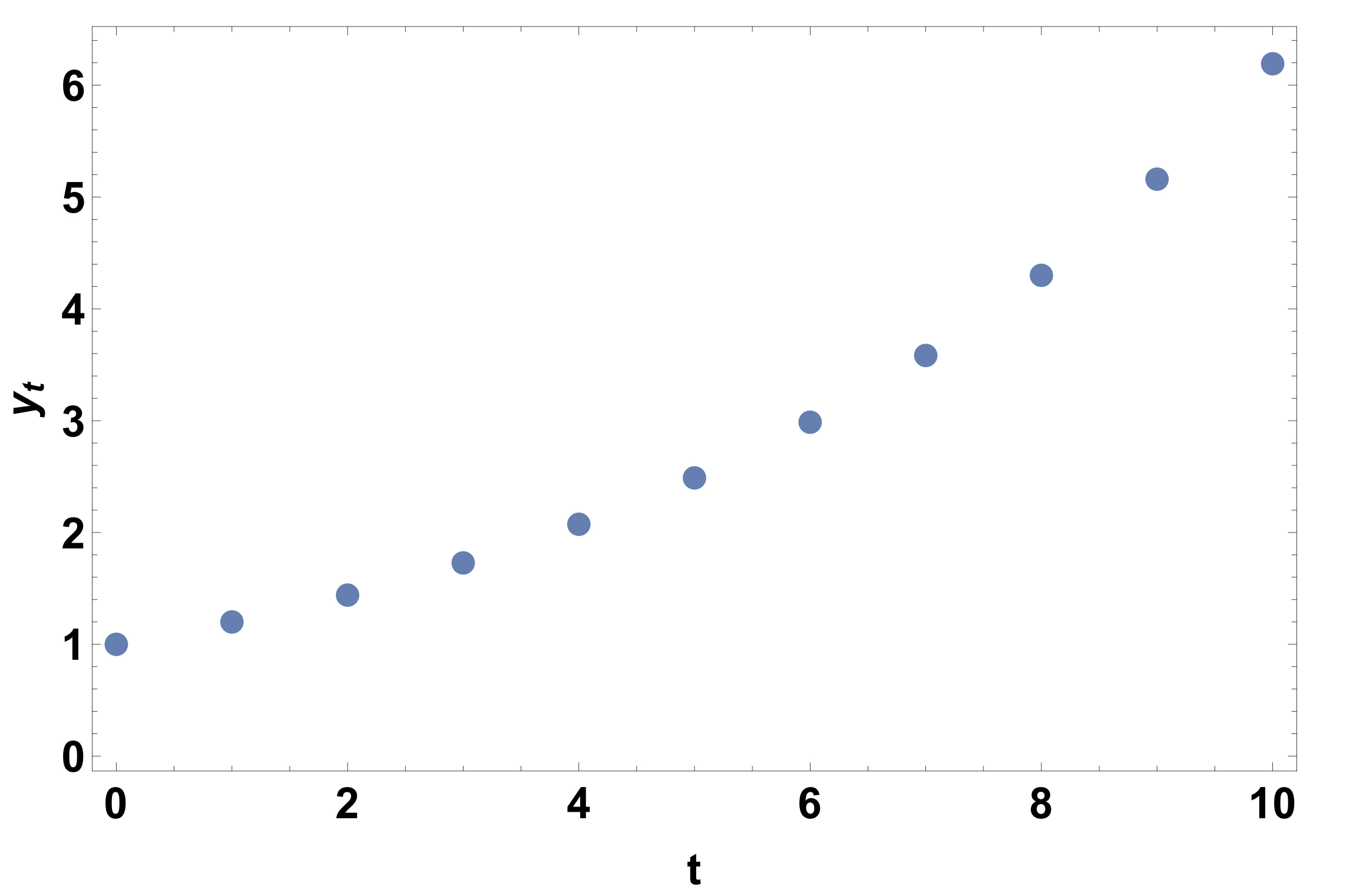
- \(y_t = \left(1.2\right)^{t}; \quad t = 0,1,2,\dots\)
We expect this to grow as \(1.2 > 1\). So \(\left(1.2\right)^{t}\) will get larger for increasing powers of \(t\). The recurrence relation can be generated from the above difference equation by indexing across the discrete variable \(t\) to get
\[\begin{align*}
y_0 &= \left(1.2\right)^{0}=1,\\
y_1 &= \left(1.2\right)^{1}=1.2,\\
y_2 &= \left(1.2\right)^{2}=1.44,\\
& \vdots
\end{align*}\]
This can be graphed to get
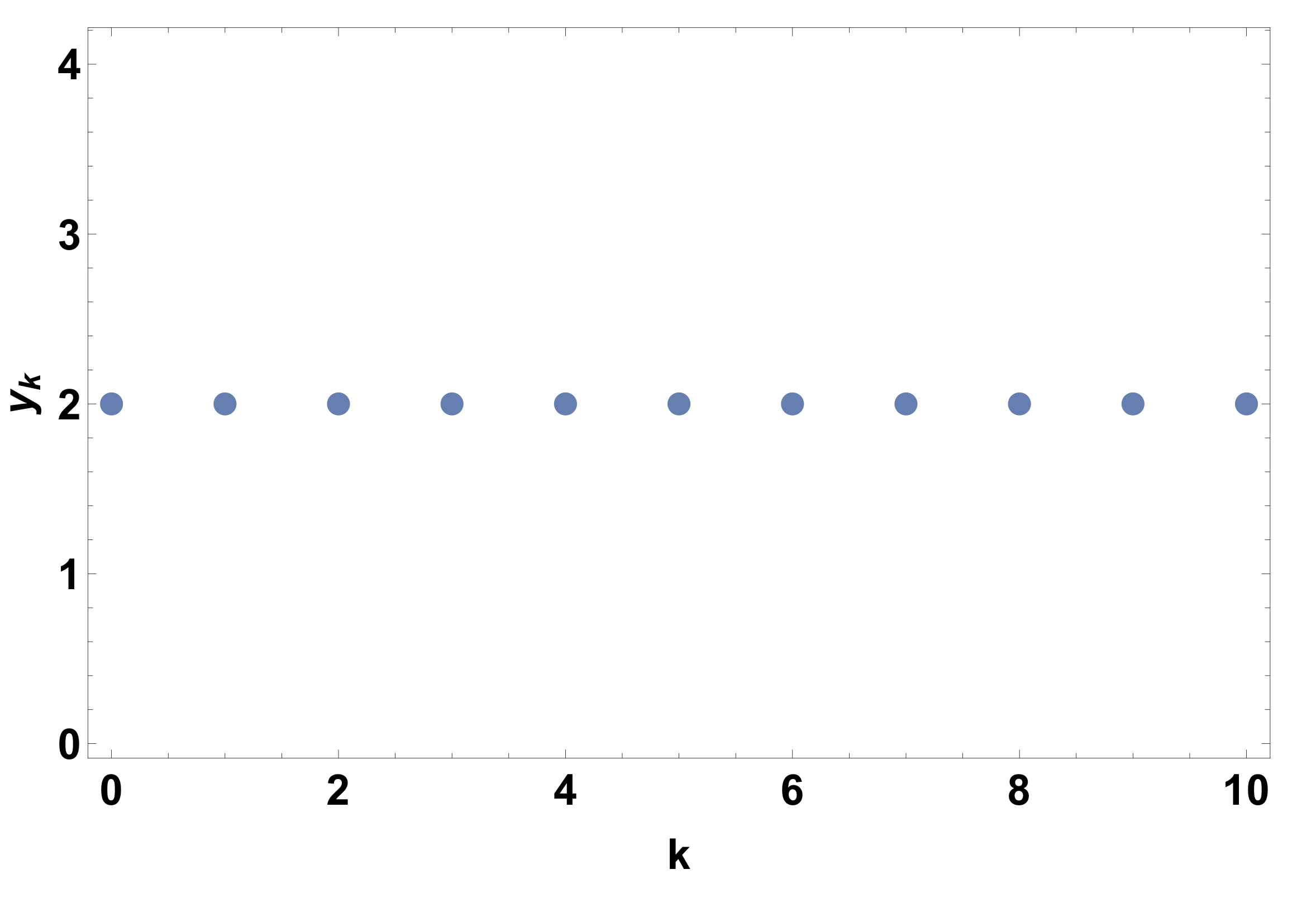
- \(y_k = 2\)
We expect this to remain unchanged as the discrete variable \(k\) does not appear explicitly in the difference equation, and so,
\[\begin{align*}
y_0 &= 2,\\
y_1 &= 2,\\
y_2 &= 2,\\
& \vdots
\end{align*}\]
This can be graphed to get
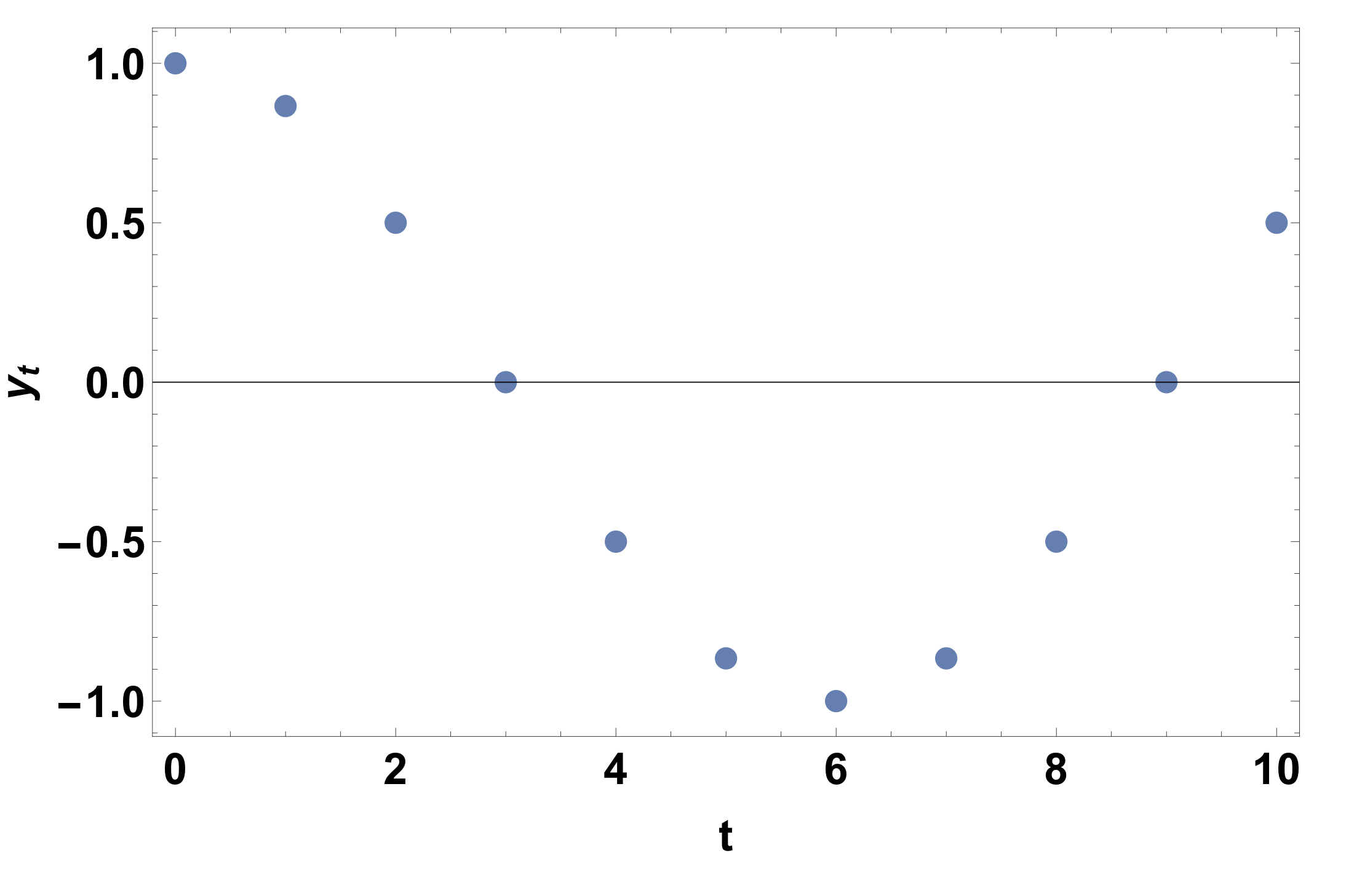
- \(y_t = \cos\left(\frac{t\pi}{6}\right); \quad t = 0,1,2,\dots\)
The recurrence relation can be generated from the above difference equation by indexing across the discrete variable \(t\) to get
\[\begin{align*}
y_0 &= \cos\left(\frac{0\pi}{6}\right)=1,\\
y_1 &= \cos\left(\frac{1\pi}{6}\right)=0.86\dots,\\
y_2 &= \cos\left(\frac{2\pi}{6}\right)=0.5,\\
& \vdots
\end{align*}\]
This can be graphed to get
Exercise
Sketch the graphs of the following discrete functions:
\(y_k = \left(-\frac{3}{4}\right)^{k}; \quad k = 0,1,2,\dots\)
\(y_t = (-1)^{t}; \quad t = 0,1,2,\dots\)
\(y_k = \left(-\frac{4}{3}\right)^{k}; \quad k = 0,1,2,\dots\)
\(y_k = \sin\left(\frac{k\pi}{6}\right);\quad k = 0,1,2,\dots\)
4.4 Classification of an Ordinary Difference Equation
Consider the general \(n\)-th order linear difference equation with constant coefficients which takes the form \[\begin{equation} a_{n} x_{k + n} + a_{n-1} x_{k + n - 1} + a_{n-2} x_{k + n - 2} + \dots + a_{1} x_{k + 1} + a_{0} x_{k} = f(k), \tag{4.2} \end{equation}\] where \(a_1, a_2,\dots,\) are coefficients different from 0 and \(\{a_{i}\}\) are independent of \(x_{k}\), \(k\) the discrete independent variable \(k = 0, 1, 2, \dots, n\), \(y_k\) the dependent variable, and \(f(k)\) is any function of \(k\).
We are interested in distinguishing all resultant difference equations that can be extracted from the above general difference equation from each other by considering some of its constituent features. As with differential equations, one can refer to the order of a difference equation, note whether it is linear or non-linear, whether it is homogeneous or non-homogeneous, or whether it has constant or variable coefficients.
4.4.1 Order
4.4.2 Linearity
4.4.3 Homogeneity
4.4.4 Coefficients
4.4.1 Classification by order
Since recurrence relations are usually written in terms of \(x_{k}\), Definition 4.3 implies that the order of a difference equation is the difference between the largest and smallest subscripts of the dependent variable appearing in the equation.
The order of Equation (4.1) is \(1\) or it is of the \(1\)st order, since \(n+1-n=1\).
The order of Equation (4.2) is \(n\) or it is of the \(n\)th order, since \(k+n-k=n\).
Examples
The difference equation \[\begin{equation*} x_{k + 1} - 2 x_{k} + 2 x_{k - 1} = 2k - 1, \end{equation*}\] has order \((k + 1) - (k - 1) = 2\). It is \(2\)nd order.
The recurrence relation \[\begin{equation*} \frac{x_{k}}{x_{k - 1}} = 2^{k}, \end{equation*}\] has order \((k) - (k - 1) = 1\). It is \(1\)st order.
The difference equation \[\begin{equation*} \sin{x_{k} - x_{k - 1}} = 5 \cos{x_{k + 2}}, \end{equation*}\] has order \((k + 2) - (k - 1) = 3\). It is \(3\)rd order.
4.4.2 Classification by linearity
Definition 4.4 (Linearity of an Ordinary Difference Equation) A difference equation is linear if the dependent variable \(y_k\) appears at most once in each term of the difference equation.
A difference equation that is not linear is said to be non-linear and this occurs when the above does not hold, that is, the dependent variable occurs more than once in any term of the equation.
Equation (4.1) is linear as the dependent variable \(x_n\) occurs only once in each term of the difference equation. Likewise, Equation (4.2) is linear as the dependent variable \(x_k\) occurs only once in each term of the difference equation.
Examples
The difference equation \[\begin{equation*} x_{k + 1} - 2 x_{k} + 2 x_{k - 1} = 2k - 1, \end{equation*}\] is linear as the dependent variable \(x_k\) appears at most once in each term of the equation.
The recurrence relation \[\begin{equation*} y_{r + 2} - 2 y_{r+1} + 3y_{r} = 2r^2, \end{equation*}\] is linear as the dependent variable \(y_r\) appears at most once in each term of the equation. Note that the term \(2r^2\) does not make the difference equation non-linear as it is non-linear in the independent discrete variable \(r\).
The difference equation \[\begin{equation*} \sin{x_{k} - x_{k - 1}} = 5 \cos{x_{k + 2}}, \end{equation*}\] is non-linear due to the appearance of transcendental functions of the dependent variable \(x_k\).
4.4.3 Classification by homogeneity
Definition 4.5 (Homogeneity of an Ordinary Difference Equation) A difference equation is homogeneous with respect to the dependent variable (say \(y_k\), in this case) if it remains invariant under a scalar transformation of the dependent variable.
In other words, replacing the dependent variable with a non-zero arbitrary constant multiplied by the dependent variable does not change the structure of the difference equation. We say that the differential equation remains invariant under this transformation.
Otherwise, the difference equation is said to be non-homogeneous with respect to the dependent variable (in this case, \(y_k\)).
Otherwise stated, the difference equation is homogeneous in the dependent variable if the substitution of \(cy_k\) (where \(c \neq 0\)) for \(y_k\) in the difference equation does not change the equation. We will refer to this as the test for homogeneity for a difference equation. Any difference equation that changes upon implementing the test will be classified as non-homogeneous.
We now implement the test for homogeneity on Equation (4.1) to check if this equation is homogeneous or not. To do this, let \(x_n=kx_n\), and so \(x_{n+1}=kx_{n+1}\). Equation (4.1) becomes
\[\begin{equation*}
kx_{n+1}=1.02kx_n.
\end{equation*}\]
Recall that \(k\) is a non-zero constant, i.e. \(k\neq 0.\) And so,
\[\begin{equation*}
x_{n+1}=1.02x_n.
\end{equation*}\]
Thus, we can conclude that Equation (4.1) is homogeneous as the structure remains unchanged, i.e. the equation remains invariant.
Let us now clarify or refine this definition for homogeneity for linear ordinary difference equations.
Definition 4.6 (Homogeneity of a Linear Ordinary Difference Equation) Consider the \(nth\)-order linear difference given in Equation (4.2): \[\begin{equation} a_{n} x_{k + n} + a_{n-1} x_{k + n - 1} + a_{n-2} x_{k + n - 2} + \dots + a_{1} x_{k + 1} + a_{0} x_{k} = f(k), \tag{4.2} \end{equation}\] where \(a_1, a_2,\dots,\) are coefficients different from 0 and \(\{a_{i}\}\) are independent of \(x_{k}\), \(k\) the discrete independent variable \(k = 0, 1, 2, \dots, n\), \(y_k\) the dependent variable, and \(f(k)\) is any function of \(k\).
Equation (4.2) is non-homogeneous with respect to the dependent variable (\(x_k\), in this case) if \(f(k) \neq 0\), in other words the sequence \(\{f(k)\}\) is not identically zero and the difference equation contains terms that are functions of the discrete independent variable \(k\) only, including constants.
Now consider the case when \(f(k)=0\), that is \[\begin{equation} a_{n} x_{k + n} + a_{n-1} x_{k + n - 1} + a_{n-2} x_{k + n - 2} + \dots + a_{1} x_{k + 1} + a_{0} x_{k} = 0. \tag{4.3} \end{equation}\] An \(nth\)-order linear ODE such as in Equation (4.3) is homogeneous with respect to the dependent variable (\(x_k\), in this case) if \(f(k)=0\), in other words it does not contain any term that is a function of the discrete independent variable \(k\) only, including constants.
Based on the above refined definition for homogeneity for linear ordinary difference equations, Equation (4.1) is a homogeneous first-order linear ordinary difference equation since \(f(k)=0\).
4.4.4 Classification by coefficients
Definition 4.7 (Coefficients of an Ordinary Difference Equation) The coefficient of any term of a difference equation is that factor of the term which does not involve the unknown discrete function. An ordinary difference equation can have constant or variable (non-constant) coefficients.
An ordinary difference equation has constant coefficients if all terms in the equation involving the dependent variable \(y_k\) are preceded by coefficients that are constants, or functions of the dependent variable only.
An ordinary difference equation has variable coefficients if at least one of the terms in the equation involving the dependent variable \(y_k\) are preceded by coefficients that are functions of the discrete independent variable \(k\).
Equation (4.1) has constant coefficients. The coefficients of \(x_{n+1}\) is 1, and \(x_n\) is \(1.02\), both of which are constants.
Classification of Differential Equations: Examples
- \(2y_{r+3}-ry_r=0\)
- \(y_ry_{r+2}-2y^3_{r-2}=r^2\)
- \(r^2y_{r + 5} + r!\: y_{r-4} =5\)
- \(y_{r + 2} - 2 y_{r+1} + 3y_{r} = 2r^2\)
Exercise
Consider the equations in Questions 1-19 given below. Check if they are difference equations, and then classify them in terms of their order, linearity, homogeneity, and coefficients.
\(3y_{r+1}+y_r=0\)
\(4x_{n+2} =4x_{n+1}+3x_n\)
\(y_n=2y_{n−1}+3y_{n−2}\)
\(2x_r−5x_{r−1}+2x_{r−2}=0\)
\(4y_{k+2}+4y_{k+1}+y_k =k^2\)
\(x_{r+2}+x_r =0\)
\(x_{r+2}−4x_{r+1}+16x_r=4·2^r+26\)
\(y_{k+2}−7y_{k+1}+10y_k =0\)
\(y_{k+2}−7y_{k+1}+10y_k = 12·4^k\)
\(y_{k+2}−7y_{k+1}+10y_k = 12·5^k\)
\(2y_{n+3}=7y_{n+2}−4y_{n+1}−4y_n\)
\(y_{k+2}−4y_k=9k^2\)
\(y_{k+3}+6y_{k+2}+11y_{k+1}+6y_k=0\)
\(x_r−4x_{r−1}+13x_{r−2}=0\)
\(y_{r+3}−6y_{r+2}+12y_{r+1}−8y_r=0\)
\(x_{r+3} =5x_{r+2} −9x_{r+1} +5x_r +4\)
\(x_{r+1} =(r+1)x_r +(r+1)!\)
\(y_{k+1}=(k+1)y_k+(k+1)!\)
\(x_{r+1} = \dfrac{x_r}{1+x_r}\)
Did you get it?
Check your understanding of some of the concepts covered in this Chapter by attempting the DYGIT? on Classification for Difference Equations. This is a formative assessment task and does not count for marks so please do it on your own to ascertain your own learning.
4.5 Methods of Solution for Ordinary Difference Equations
The theory of solving linear difference equations such as Equation (4.2) is similar to that for solving linear ODEs as seen in Chapter 2. Indeed, there are equivalent definitions and methods in the theory of recurrence relations to those in the theory of differential equations.
We will consider two particular methods of solution for ordinary differential equations in this course:
4.5.1 The Direct Method
4.5.2 The Method of Undetermined Coefficients
These are just two analytical methods for finding solutions to difference equations. There are other analytical and numerical methods you will encounter in Mathematics, Physics, and further studies in Applied Mathematics.
4.5.1 The Direct Method
This method involves a brute force approach. Given some difference equation with an initial condition:
- Generate the sequence from the difference equation using the given initial condition.
- Look for an emerging pattern.
- Use this pattern to write down a possible solution, known as a recurrence relation.
Examples
Use the direct method to find a solution to the given difference equation
- \(y_k=2y_{k-1} \quad \text{given} \: \: y_0\)
- \(y_{k+1}=(k+1)y_{k} \quad \text{given} \: \: y_0\)
4.5.2 The Method of Undetermined Coefficients
This method is analogous to the method used to solve differential equations. It follows the same general procedure, with a few specified differences. We consider linear difference equations with constant coefficients. We first find the complementary function \(y^c_k\) of the corresponding homogeneous difference equation. We then use a suitable ansatz to find the particular integral \(y^p_k\) using the method of undetermined coefficients. We can then construct the general solution \(y_k=y^c_k+y^p_k\). Finally we can then use given initial conditions \(y_0,\:y_1,\dots,\) to find the values of the arbitrary constants, and thus find a particular solution.
4.5.2.1 Homogeneous Linear Difference Equations with Constant Coefficients
Here we demonstrate that the familiar techniques of solving linear ODEs apply in a similar manner to solve linear difference equations or recurrence relations. First consider the difference equation \[\begin{equation*} x_{k + 1} - a x_{k} = 0, \end{equation*}\] where \(a\) is independent of \(k\). This is a first order, linear, homogeneous difference equation. Notice that this equation implies that the \((k+1)\)-th term in the sequence is proportional to the \(k\)-th term in the sequence \(\{x_{k}\}\). Incrementing \(k\) yields \[\begin{align*} x_{k+1} &= a x_{k}, \\ x_{k+2} &= a x_{k+1} = a^{2} x_{k}, \\ x_{k+3} &= a x_{k+2} = a^{3} x_{k}, \\ & \vdots \\ x_{k+n} &= a^{n} x_{k}. \end{align*}\] Clearly, given some initial condition \(x(0) = x_{0}\), we have \[\begin{equation*} x_{k} = x_{0} a^{k}. \end{equation*}\] The parameter appearing in the original difference equation appears as a parameter in the solution. Note the appearance of the exponential term \(a^{k}\) in the solution. This is a common pattern that arises in solutions to linear difference equations that have terms proportional to terms appearing earlier in the sequence. We shall use this to construct solutions to linear differential equations with constant coefficients.
Consider the second order linear difference equation \[\begin{equation} a x_{k + 2} + b x_{k + 1} + c x_{k} = 0, \tag{4.4} \end{equation}\] where \(a\), \(b\), and \(c\) are constants. To solve this equation, select a suitable trial solution of the form \(x_{k} = A \lambda^{k}\), where \(\lambda\) is a yet to be determined constant. Thus, \(x_{k+1} = A \lambda^{k+1}=A \lambda \lambda^{k}\), and \(x_{k+2} = A \lambda^{k+2}=A \lambda^{2} \lambda^{k}\). Direct substitution of the trial solution into (4.4) yields an algebraic equation \[\begin{equation*} A \left( a \lambda^{2} + b \lambda + c \right) \lambda^k = 0. \end{equation*}\] Since we require non-trivial solutions, \(A\) and \(\lambda^k\) are not identically zero, and we conclude that \[\begin{equation} a \lambda^{2} + b \lambda + c = 0. \tag{4.5} \end{equation}\] We call (4.5) the characteristic equation or auxiliary equation of the homogeneous equation (4.4). The roots of (4.5) are \[\begin{equation*} \lambda_{1} = \dfrac{-b - \sqrt{b^{2} - 4 a c}}{2a} \quad \text{and} \quad \lambda_{2} = \dfrac{-b + \sqrt{b^{2} - 4 a c}}{2a}. \end{equation*}\] The nature of the solutions of (4.5) depend on the values \(\lambda_{1}\) and \(\lambda_{2}\) and we shall examine each separately. In each case, consider the behaviour of the discriminant of (4.5), for the cases that \(b^{2} - 4 a c\) is positive, negative or zero.
Consider the following cases:
Case 1: Distinct real roots \(b^{2} - 4 a c > 0\)
Here, \(\lambda_{1}\) and \(\lambda_{2}\) are real and distinct and (4.5) has two distinct solutions, \[\begin{equation*} x_{1}(k) = \lambda_{1}^{k} \quad \text{and} \quad x_{2}(k) = \lambda_{2}^{k} \end{equation*}\] Since (4.4) is second order it must contain two arbitrary constants. Additionally, (4.4) is linear and homogeneous, so by the superposition principle, any linear combination of two solutions is also a solution. Hence, the general solution to Equation (4.4) is \[\begin{equation*} x_k = x^c_k = c_{1} \lambda_{1}^{k} + c_{2} \lambda_{2}^{k}. \end{equation*}\] with \(c_{1}\) and \(c_{2}\) as arbitrary constants.
Example
Consider the following equation, \[\begin{equation*} x_{k} - 3 x_{k - 1} - 4 x_{k-2} = 0. \end{equation*}\]
Let the trial solution take the form \(x_k = A \lambda^{k}\). Thus, \(x_{k-1} = A \lambda^{k-1}=A\frac{\lambda^{k}}{\lambda}\), and \(x_{k-2} = A \lambda^{k-2}=A\frac{\lambda^{k}}{\lambda^2}\).
Then direct substitution of the trial solution into the given difference equation yields \[\begin{equation*} A \lambda^{k} - 3 A\frac{\lambda^{k}}{\lambda} - 4A\frac{\lambda^{k}}{\lambda^2} = 0. \end{equation*}\] Simplifying, \[\begin{equation*} A \lambda^{k}\left(1 - 3 \frac{1}{\lambda} - 4\frac{1}{\lambda^2}\right) = 0. \end{equation*}\] Since \(A \neq 0\), and \(\lambda^k \neq 0\), it follows that for the above equation to hold, we must have that \[\begin{equation*} 1 - 3 \frac{1}{\lambda} - 4\frac{1}{\lambda^2} = 0. \end{equation*}\] We can multiply each term by \(\lambda^2\), and thus the auxiliary equation is \[\begin{equation*} \lambda^{2}- 3 \lambda - 4 = 0, \end{equation*}\] with roots \(\lambda_{1} = -1\) and \(\lambda_{2} = 4\). Hence, the complementary function, which in this case is the general solution, is \[\begin{equation*} x_k = x^c_k = c_{1} (-1)^{k} + c_{2} (4)^{k}, \end{equation*}\] where \(c_{1}\) and \(c_{2}\) are arbitrary constants.
Case 2: Repeated real roots \(b^{2} - 4 a c = 0\)
The roots of (4.5) coincide and \(\lambda_{1} = \lambda_{2} = \lambda = -\frac{b}{2a}\), so there exists a solution \[\begin{equation*} x_{1}(k) = \lambda^{k}. \end{equation*}\] Since the difference equation is second order, and must contain two arbitrary constants, we conclude that there must exist a second solution \(x_{2}(k)\). To determine this second solution, consider a second trial solution \(x_k = Bk \lambda^{k}\), which is similar to, but linearly independent of the first trial solution. Direct substitution of this trial solution into (4.4) yields \[\begin{equation*} aB(k + 2) \lambda^{k + 2} + bB(k + 1) \lambda^{k + 1} + cB k \lambda^{k} = 0, \end{equation*}\] and collecting like terms and factorizing yields, \[\begin{align*} 0 &= B \lambda^{k} \left( a(k + 2) \lambda^{2} + b(k + 1) \lambda + c k \right), \\ 0 &= B \lambda^{k} \left( (a \lambda^{2} + b \lambda + c) k + 2 a \lambda^{2} + b \lambda \right). \end{align*}\] Note, however that \(a \lambda^{2} + b \lambda + c = 0\), so \[\begin{equation*} 0 = 2 a \lambda^{2} + b \lambda. \end{equation*}\] It follows that either \(\lambda = 0\) or \(2 a \lambda + b = 0\). Since we require non-trivial solutions, we discard \(\lambda = 0\) and take instead \(\lambda = - \frac{b}{2a}\). The second solution is \[\begin{equation*} x_{2}(t) = k \lambda^{k}. \end{equation*}\] Combine \(x_{1}\) and \(x_{2}\) to form the general solution, \[\begin{equation*} x_k = x^c_k = c_{1} \lambda^{k} + c_{2} k \lambda^{k}, \end{equation*}\] or \[\begin{equation*} x_k = x^c_k = \left( c_{1} + c_{2} k \right) \lambda^{k} \end{equation*}\] with \(c_{1}\) and \(c_{2}\) as arbitrary constants.
Example
Consider the following equation, \[\begin{equation*} x_{k} - 4 x_{k-1} + 4 x_{k-2} = 0, \end{equation*}\]
Take \(x_k = A \lambda^{k}\) as the trial solution. Thus, \(x_{k-1} = A \lambda^{k-1}=A\frac{\lambda^{k}}{\lambda}\), and \(x_{k-2} = A \lambda^{k-2}=A\frac{\lambda^{k}}{\lambda^2}\).
Upon substitution we get \[\begin{equation*} A \lambda^{k} - 4 A\frac{\lambda^{k}}{\lambda} + 4A\frac{\lambda^{k}}{\lambda^2} = 0. \end{equation*}\] Simplifying, \[\begin{equation*} A \lambda^{k}\left(1 - 4 \frac{1}{\lambda} + 4\frac{1}{\lambda^2}\right) = 0. \end{equation*}\]
Since \(A \neq 0\), and \(\lambda^k \neq 0\), it follows that for the above equation to hold, we must have that \[\begin{equation*} 1 - 4 \frac{1}{\lambda} + 4\frac{1}{\lambda^2} = 0. \end{equation*}\] We can multiply each term by \(\lambda^2\), and thus the associated auxiliary equation is \[\begin{equation*} \lambda^{2} - 4 \lambda + 4 = 0, \end{equation*}\] with a double root \(\lambda = 2\). Therefore, one solution to this difference equation is \[\begin{equation*} x_{1}(k) = 2^{k}. \end{equation*}\] A second solution to this difference equation is \[\begin{equation*} x_{2}(k) = k 2^{k}. \end{equation*}\] Combining \(x_{1}\) and \(x_{2}\) yields the complementary function, which in this case is the general solution, \[\begin{equation*} x_k=x^c_k = c_{1} 2^{k} + c_{2} k 2^{k}. \end{equation*}\]
The appearance of a second solution, which is equal to the product of some function of the independent variable and the first solution, is also a common feature of difference equations with zero discriminant. Something similar was encountered in our study of ODEs.
Case 3: Complex conjugate roots \(b^{2} - 4 a c < 0\)
Here, \(\lambda_{1}\) and \(\lambda_{2}\) are complex conjugate roots of the auxiliary equation (4.5). Hence, (4.4) has two distinct solutions: the conjugate root pair \(\lambda_{1} = \alpha + i \beta\) and \(\lambda_{2} = \alpha - i \beta\), where \(i \equiv \sqrt{-1}\). We can now rewrite \(x_{1}\) as \[\begin{equation*} x_{1}(k) = (\alpha + i \beta)^{k}. \end{equation*}\] Similarly, rewrite \(x_{2}\) as \[\begin{equation*} x_{2}(k) = (\alpha - i \beta)^{k}. \end{equation*}\] Again, since (4.4) is second order, it must contain two arbitrary constants. Also, by the linearity and homogeneity of (4.4), the superposition principle implies that any linear combination of these two solutions is a solution. Hence, the general solution to (4.4) is \[\begin{equation*} x_k = x^c_k = c_{1} (\alpha + i \beta)^{k} + c_{2} (\alpha - i \beta)^{k}. \end{equation*}\] with \(c_{1}\) and \(c_{2}\) as arbitrary constants.
We would like to rewrite these solutions in a more natural way, free of the complex numbers associated with the negative discriminant. To do this, define, \[\begin{equation*} \alpha = -\frac{b}{2a} \quad \text{and} \quad \beta = \frac{\sqrt{4 a c - b^{2}}}{2a}. \end{equation*}\] Recall the Euler identity, \[\begin{equation} z_{\pm} = \alpha \pm i \beta = \sqrt{\alpha^{2} + \beta^{2}} e^{\pm i \theta}, \end{equation}\] where, \[\begin{equation*} \theta = \arctan{\frac{\beta}{\alpha}}. \end{equation*}\] Rewriting the general solution using the Euler identity yields \[\begin{align*} x_k &= c_{1} (\alpha + i \beta)^{k} + c_{2} (\alpha - i \beta)^{k} \\ &= c_{1} \left( \sqrt{\alpha^{2} + \beta^{2}} e^{i \theta} \right)^{k} + c_{2} \left( \sqrt{\alpha^{2} + \beta^{2}} e^{- i \theta} \right)^{k} \\ &= \left( \alpha^{2} + \beta^{2} \right)^{\frac{k}{2}} \left( c_{1} e^{i k \theta} + c_{2} e^{- i k \theta} \right). \end{align*}\] Let \(R = \sqrt{\alpha^{2} + \beta^{2}}\), then by the Euler identity, \[\begin{equation*} x_k = R^{k} \left( ( c_{1} + c_{2} ) \cos{k \theta} + i ( c_{1} - c_{2} ) \sin{k \theta} \right). \end{equation*}\] Define, \(c_{3} = c_{1} + c_{2}\) and \(c_{4} = i(c_{1} - c_{2})\), then \[\begin{equation} x_k = x^c_k = R^{k} \left[ c_{3} \cos{k \theta} + c_{4} \sin{k \theta} \right], \end{equation}\] where \(c_{3}\) and \(c_{4}\) are to be determined constants.
Example
Consider the following equation, \[\begin{equation*} x_{k + 2} - 2 x_{k + 1} + 2 x_{k} = 0. \end{equation*}\]
Let the trial solution take the form \(x_k = A \lambda^{k}\). Thus, \(x_{k+1} = A \lambda^{k+1}=A\lambda\lambda^{k}\), and \(x_{k+2} = A \lambda^{k+2}=A\lambda^2\lambda^{k}\).
Then direct substitution of the trial solution into the given difference equation yields \[\begin{equation*} A\lambda^2\lambda^{k}-2 A\lambda\lambda^{k} + 2 A \lambda^{k} = 0. \end{equation*}\] Simplifying, \[\begin{equation*} A \lambda^{k}\left(\lambda^2 - 2 \lambda + 2 \right)= 0. \end{equation*}\]
Since \(A \neq 0\), and \(\lambda^k \neq 0\), it follows that for the above equation to hold, we must have that \[\begin{equation*} \lambda^{2} - 2 \lambda + 2 = 0. \end{equation*}\]
This is the associated auxiliary equation with roots \(\lambda_{1} = 1 - i\) and \(\lambda_{2} = 1 + i\). Hence, the complementary function, which in this case is the general solution, is \[\begin{equation*} x_k = x^c_k = c_{1} (1 - i)^{k} + c_{2} (1 + i)^{k}, \end{equation*}\] with \(c_{1}\) and \(c_{2}\) as arbitrary constants. Note, however, that with \(\alpha=1\) and \(\beta=1\), we get that \[\begin{equation*} R = \sqrt{2} \quad \text{and} \quad \theta = \arctan{1} = \frac{\pi}{4}, \end{equation*}\] so, the general solution becomes \[\begin{equation*} x_k = x^c_k = 2^{\frac{k}{2}} \left[ c_{3} \sin \left(\frac{k\pi}{4}\right) + c_{4} \cos \left(\frac{k\pi}{4}\right) \right], \end{equation*}\] where \(c_{3}\) and \(c_{4}\) are arbitrary constants.
Notice that the general solution is now a product of an exponential term and a pair of trigonometric functions. This is a common feature of homogeneous difference equations with negative discriminant.
Additional Examples
- \(y_{k} - 3 y_{k - 1} - 4 y_{k-2} = 0;\) given \(y_0=10\) and \(y_1=15\)
- \(x_{k + 2} - 4 x_{k + 1} + 4 x_{k} = 0;\) given \(x_0=3\) and \(x_1=10\)
- \(x_{r + 2} +4 x_{r + 1} + 9 x_{r} = 0\)
4.5.2.2 Undetermined Coefficients: Superposition Approach
Similar to the case of general linear non-homogeneous ODEs, the general solution \(x_k\) of the general linear non-homogeneous difference equation comprises the complementary function \(x^c_{k}\) and the particular integral \(x^p_{k}\) such that \[\begin{equation} x_k = x^c_{k} + x^p_{k}, \end{equation}\] where \(x^c_{k}\) is the solution to the homogeneous part of the difference equation. We may find a trial solution for \(x^c_{k}\) by inspecting the homogeneous part of the RR. This process will introduce \(n\) arbitrary constants into the solution. The complementary function contains \(n\) arbitrary constants which are determined by initial conditions.
In contrast, we may make an educated guess or ansatz for \(x^p_{k}\) by inspecting the non-homogeneous term \(f(k)\), and comparing this with the complementary function \(x^c_{k}\) for possible duplication. We follow the same method, procedure, and steps as was applied to ODEs.
This is illustrated in the following examples.
Examples
- Consider the recurrence relation \[\begin{equation*} y_{k+2} - 3 y_{k+1} - 4 y_{k} = 5. \end{equation*}\] The homogeneous part of this equation is \[\begin{equation*} y_{k+2} - 3 y_{k+1} - 4 y_{k} = 0. \end{equation*}\] Choosing \(y_k = A \lambda^{k}\) as a trial solution yields the corresponding auxiliary equation, \[\begin{equation*} \lambda^{2} - 3 \lambda - 4 = 0, \end{equation*}\] which has roots \(\lambda_{1} = -1\) and \(\lambda_{2} = 4\). From these roots we construct the complementary function \[\begin{equation*} y^c_{k} = c_{1} (-1)^{k} + c_{2} 4^{k}. \end{equation*}\]
To construct the particular integral, choose \(y^p_{k} = C\) as the ansatz for the particular solution since \(f(k)=5\), which is a constant. Thus, \(y^{p}_{k+1} = C\), and \(y^{p}_{k+2} = C\). This choice upon substitution into the original difference equation yields the equation \[\begin{equation*} C - 3 C - 4 C = 5. \end{equation*}\] So \(C= - \frac{5}{6}\). This gives the particular integral, \[\begin{equation*} y^p_{k} = - \frac{5}{6}. \end{equation*}\] Hence, the general solution is \[\begin{equation*} y_k = y^c_{k} + y^p_{k} = c_{1} (-1)^{k} + c_{2} 4^{k} - \frac{5}{6}. \end{equation*}\]
Consider the difference equation \[\begin{equation*} x_{k} - x_{k-1} = 2^{k}. \end{equation*}\] The homogeneous part of this equation is \[\begin{equation*} x_{k} - x_{k-1} = 0. \end{equation*}\] Choosing \(x_k = A\lambda^{k}\) as a trial solution yields the corresponding auxiliary equation, \[\begin{equation*} \lambda - 1 = 0, \end{equation*}\] The complementary function is then \[\begin{equation*} x^c_{k} = c_{1} 1^{k} = c_{1}. \end{equation*}\] Choose \(x^p_{k} = A 2^{k}\) as the ansatz for the particular integral since \(f(k)=2^k\).Thus \(x^p_{k-1} = A 2^{k-1}\). This choice upon substitution into the original difference equation yields the equation \[\begin{equation*} A 2^{k} - A 2^{k-1} = 2^{k}, \end{equation*}\] or \[\begin{equation*} 2^{k-1} \left( A - 2 \right)= 0. \end{equation*}\] So, \(A= 2\). This gives the particular integral, \[\begin{equation*} x^p_{k} = 2.2^k= 2^{k+1}. \end{equation*}\] Hence, the general solution is \[\begin{equation*} x_k = x^c_{k} + x^p_{k} = c_{1} + 2^{k+1}. \end{equation*}\]
\(x_k-x_{k-1}=2k\)
Notice that Examples 2 and 3 above are identical, except for \(f(k)\). This subtle change results in a more complex solution for the particular integral in Example 3 as there was duplication in the choice of the ansatz and the complementary function. Example 3 gives rise to the following important Theorem:
Theorem 4.1 (Duplication between \(y^p_k\) and \(y^c_k\)) The following theorem outlines the cases with and without duplication:
Suppose that the linear non-homogeneous difference equation with constant coefficients \[\begin{equation} a_{n} x_{k + n} + a_{n-1} x_{k + n - 1} + a_{n-2} x_{k + n - 2} + \dots + a_{1} x_{k + 1} + a_{0} x_{k} = f(k) \tag{4.2} \end{equation}\] has \(f(k)\) that is if the form \[\begin{equation} f(k)=(b_{t} k^{t} + b_{t-1} k^{t - 1} + \dots + b_{1} k + b_{0})s^{k}, \end{equation}\] where \(b_0, b_1,\dots,b_t\) and \(s\) are real numbers.
If \(s\) is not a characteristic root of the associated linear homogenous difference equation of Equation (4.2) that leads to the complementary function \(y^c_k\), the ansatz \(y^p_k\) for the particular integral is of the form \[\begin{equation} y^p_k=(c_{t} k^{t} + c_{t-1} k^{t - 1} + \dots + c_{1} k + c_{0})s^{k}. \end{equation}\]
If \(s\) is a characteristic root of the associated linear homogenous difference equation of Equation (4.2) with multiplicity \(m\) that leads to the complementary function \(y^c_k\), the ansatz \(y^p_k\) for the particular integral is of the form \[\begin{equation} y^p_k=n^{m}(c_{t} k^{t} + c_{t-1} k^{t - 1} + \dots + c_{1} k + c_{0})s_{k}. \end{equation}\]
- \(y_{k+2}-7y_{k+1}+10y_k=12 \cdot 5^k\)
- \(x_k-x_{k-1}=k\)
Try this yourself
Exercise
Consider the difference equations in Questions 1-19 given below. Solve the given difference equation using an appropriate method.
\(3y_{r+1}+y_r=0\), given \(y_1=1\)
\(4x_{n+2} =4x_{n+1}+3x_n\), given \(x_0 =2\) and \(x_1 =1\)
\(y_n=2y_{n−1}+3y_{n−2}\), given \(y_0=5\) and \(y_1=7\)
\(2x_r−5x_{r−1}+2x_{r−2}=0\), given \(x_0=0\) and \(x_1=1\)
\(4y_{k+2}+4y_{k+1}+y_k =k^2\), given \(y_0 =0\) and \(y_1 =0\)
\(x_{r+2}+x_r =0\), given \(x_0 =1\) and \(x_1 =2\)
\(x_{r+2}−4x_{r+1}+16x_r=4·2^r+26\), given \(x_0=x_1=1\)
\(y_{k+2}−7y_{k+1}+10y_k =0\), given \(y_0 =0\) and \(y_1 =3\)
\(y_{k+2}−7y_{k+1}+10y_k = 12·4^k\), given \(y_0 = y_1 = 0\)
\(y_{k+2}−7y_{k+1}+10y_k = 12·5^k\), given \(y_0 = y_1 = 0\)
\(2y_{n+3}=7y_{n+2}−4y_{n+1}−4y_n\), given \(y_0=0\), \(y_1=1\) and \(y_2=2\)
\(y_{k+2}−4y_k=9k^2\), given \(y_0 = y_1 = 0\)
\(y_{k+3}+6y_{k+2}+11y_{k+1}+6y_k=0\), given \(y_0 = y_1 = y_2 = 0\)
\(x_r−4x_{r−1}+13x_{r−2}=0\), given \(x_0=2\) and \(x_1 =1\)
\(y_{r+3}−6y_{r+2}+12y_{r+1}−8y_r=0\), given \(y_0 = y_1 = y_2 = 2\)
\(x_{r+3} =5x_{r+2} −9x_{r+1} +5x_r +4\), given \(x_0 =x_1 =−2\) and \(x_2 =0\)
\(x_{r+1} =(r+1)x_r +(r+1)!\), given \(x_0 =1\)
\(y_{k+1}=(k+1)y_k+(k+1)!\), given \(y_0=a\)
\(x_{r+1} = \dfrac{x_r}{1+x_r}\), given \(x_0\)
For what values of \(a\) are the solutions of \(y_{k+2} − 2y_{k+1} + (1 − a)y_k = 0\) oscillatory in character?
What is the character of the solutions of \(y_{k+2}−2ay_{k+1}+ay_k =0\) for
- \(0<a<1\)?
- \(a=1\)?
- \(a>1\)?
Selected Answers
\(y_r=−3\left(-\frac{1}{3}\right)^{r}\)
\(x_n=\left(-\frac{1}{2}\right)^{n}+\left(\frac{3}{2}\right)^{n}\)
\(y_n=3\left(3\right)^{n}+2\left(-1\right)^{n}\)
\(x_r=\frac{2}{3}\left[2^r-\left(\frac{1}{2}\right)^{r}\right]\)
\(y_k=\frac{1}{27}\left[-4\left(-\frac{1}{2}\right)^{k}+2k\left(-\frac{1}{2}\right)^{k}+3k^2-8k+4\right]\)
\(x_r=\cos \frac{r \pi}{2} +2 \sin \frac{r \pi}{2}\)
\(x_r=4^r\left(-\frac{4}{3}\cos \frac{r \pi}{3} +\frac{1}{2 \sqrt{3}} \sin \frac{r \pi}{3}\right)+\frac{2^r}{3}+2\)
\(y_k= 5^k - 2^k\)
\(y_k=2 \cdot 2^k +4 \cdot 5^k −6 \cdot 4^k\)
\(y_k=\frac{4}{3} \left(2^k - 5^k\right) +\frac{4}{5} k \cdot 5^k\)
\(y_n=\frac{8}{25} \cdot 2^n+\frac{1}{10} \cdot n2^n-\frac{8}{25} \cdot \left(-\frac{1}{2}\right)^{n}\)
\(y_k=\frac{27}{4} \cdot 2^k-\frac{1}{12} \cdot \left(-2\right)^k-3k^2-4k-\frac{20}{3}\)
\(y_k=3 \cdot \left(-1 \right)^k-3 \cdot \left(-2 \right)^k+\left(-3 \right)^k\)
\(x_r=13^{r/2}\left[2\cos \left(r \arctan \frac{3}{2}\right) +4 \sin \left(r \arctan \frac{3}{2}\right)\right]\)
\(y_r=2^r\left(2-\frac{5}{4}r +\frac{1}{4} r^2 \right)\)
\(x_r=\left(\sqrt{5}\right)^{r}\left[\sin \left(r \arctan \frac{1}{2}\right) -3 \cos \left(r \arctan \frac{1}{2}\right)\right]+2r+1\)
\(x_r=(r+1)!\)
\(y_k=k!(k+a)\)
\(x_r=\dfrac{x_0}{1+rx_0}\)
\(a<0\)
- Oscillatory
- Linear
- Exponential
Did you get it?
Check your understanding of some of the concepts covered in this Chapter by attempting the DYGIT? on Methods of Solution for Difference Equations. This is a formative assessment task and does not count for marks so please do it on your own to ascertain your own learning.