4 Linked Lists

4.1 Introduction

4.1.1 Arrays

So far we’ve used arrays to implement lists of objects. For example, if we wanted a list of 6 integers, we would use the following code:

int myList[6]; // Allocated on the Stack
int *myList = new int[6]; // Dynamically Allocated on the Heap

On the first line, space for the array will be reserved on the call stack when the frame for this function is created. Because the array will be inside the frame, we need to know the size of the array when the frame is allocated. This means that you can’t have a function that reads in a number and then uses the stack to allocate an array of that size, because the stack frame has already been created.⁸ On line 2, new[] will ask the operating system for 6×sizeof(int) bytes from the Heap or Freestore. The operating system will find a convenient place in RAM to reserve this memory and will return the address of the first object in the array. We store the address inside the pointer myList. We may be left with the following memory layout:

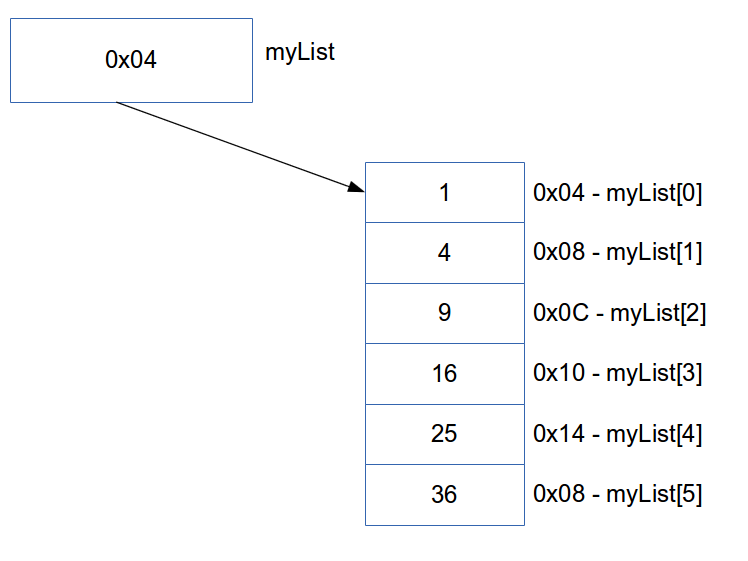
Figure 4.1: Memory Layout of an Array

Once the operating system has allocated the block of memory, the size of the block cannot be changed. If we suddenly decided that the array isn’t big enough, we would need to make a new, bigger array and then copy all the items that we need across. After copying the \(n\) items to the new memory, we would have to free the old one. For example:

int *newArray = new int[10]; // Allocate a bigger array

for(int i = 0; i < 6; i++){ // Loop over the original array
   newArray[i] = myList[i]; // Copy the values to the new array
}

delete [] myList;  // Deallocate the original array
myList = newArray; // Make the pointer point to the new one

Note: Even though the realloc function from C99 changes the size of a memory block/array, in practice, it can only make the array longer if there is free space after the original one. If there is no free space, it will allocate new memory and copy the contents across – just as shown above.

4.1.2 Questions

If you have an array of size \(n\) that needs to be increased to size \(2n\), how many copies must your program make?
If it takes \(3\) time steps to copy a single number, how long does the copy take?
If the list of \(2n\) items fills up and we now need to increase the size to \(3n\), how many copies will the program have done in total?

4.2 When arrays aren’t good enough

Let’s say that we have a program that must read numbers into an array until it reads \(-1\). We have no idea how much memory to allocate at the start of our program. If we try to allocate too much it might fail because the operating system can’t find enough contiguous space.⁹ If we allocate too little, we might waste a lot of time copying items to new arrays every time it fills up. If we had to reallocate \(4\) times, then it means the first item added to the list needs to be moved \(4\) times as well. It would be useful if we could come up with some data structure that allows us to change the size of the list without any major cost in both time and memory requirements (space).

Suppose you have a program where there is an array of \(100\) integers. I need you to insert a number at the beginning of the list and each number shifts over by one. The last number in the list is removed. To do this, you first need to move all the numbers one item to the right - list[98] moves to list[99] etc. When you have moved all the numbers in the list, you are now free to add the new item to list[0].

Suppose you have a program where you need to delete the \(i^{th}\) number in an array. While we can fetch the number in constant time¹⁰ all the numbers in the array need to be consecutive in memory. If we just removed the number and left everything where it was, we’d leave our array with a hole in the middle – this would break the array because the objects are no longer contiguous. To fix this, we need to shift every item from \(i\) onwards, one block to the left.

4.2.1 Questions

If you have an array of \(n\) items, how many ‘move/copy’ operations must you do to insert a number at the front of the list?
If you have an array of \(n\) items and you want to delete the item at the front, how many ‘move/copy’ operations must you do?
If you want to insert \(n\) items into a list that is already \(n\) items long, exactly how many ‘move/copy’ operations should you do?

4.2.2 Linked Structures

In the previous examples, we end up doing a lot of extra work because we have to make sure that the memory is contiguous but cannot ask the Operating System to allocate new memory next to the old memory. If we could come up with a new structure that didn’t require contiguous memory, then we would be able to allocate and free memory as necessary without worrying where the memory actually was and without needing to copy all the old items into the new memory each time.

The idea behind this type of structure is to allocate separate pieces of memory on the heap and then link them together like a chain, using pointers.

4.3 Linked Lists – `forward_list`

Linked lists consist of a number of links or nodes. Each one contains a value and a pointer to the next node in the list.

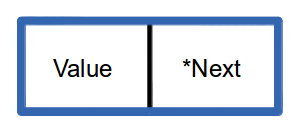
Figure 4.2: Link for a Linked List

We can code it as a class or a struct.

class Link{
public:
   int value;
   Link *next;
};

struct Link{
   int value;
   Link *next;
}

The idea is that we simply store a pointer to the first link (sometimes called a node), and then each node stores the address of the next node. So as long as we remember where the first item is, we can follow its ‘next pointer’ to get to the next link in the chain. The last link’s next pointer should contain the nullptr because there is no next link to point to.

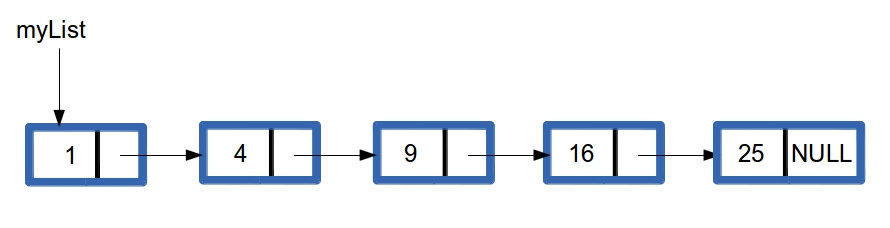
Figure 4.3: A Linked List

To create the list in Figure 4.3 we might use the following code:

class Link{
public:
   int value;
   Link *next;
   Link(int v) : value(v), next(nullptr){
      /* Initialise value with v and set next to the nullptr */
   }
};

class LinkedList{
public:
   Link* head;

   LinkedList() : head(nullptr){
      /* The line above initialises head to be the nullptr */
   }
   ~LinkedList() { 
      /* Traverse the list and deallocate each link */
   }
};

int main(){
   LinkedList myList;

   for(int i = 5; i > 0; --i){
      // Create a new link
      Link *tmp = new Link(i*i);
      // Insert at the front:
      tmp->next = myList.head;
      myList.head = tmp;
   }
   
   // Traverse the list and print each value
   Link *curr = myList.head;
   while(curr != nullptr){
      cout << curr->value << endl;
      curr = curr->next;
   }
}

Notes:

myList is an instance of the LinkedList class.
It contains a pointer that always points to the head of the list – the first link.
By keeping a pointer to the head, we can easily insert items into the front of the list.
The next pointer in the last node must contain the nullptr so that we know when to stop during a traversal.
To get to any item in the list we need to traverse the list from the head. We do this by repeatedly following the next pointers until we reach the desired node.
Note that the myList (i.e. the instance of LinkedList, which is an object containing only a single pointer) is an automatic variable that is allocated on the stack. It is part of the stack frame for the main function. All the individual Link instances are dynamically allocated using the new keyword, so those objects live on the heap.
When the list is destroyed we should make sure we clean up any memory that we have allocated to avoid memory leaks. The LinkedList destructor should traverse the list deallocating all the links that were allocated using new. The list itself (myList) was automatically allocated on the stack, so we do not manually free that memory.
Just like with a chain, if we break a link we will lose access to the links that follow it. We need to be careful to avoid memory leaks, so we need to copy the value of the current link’s next pointer before we delete it. Otherwise, we would drop the rest of the chain and would not be able to free the remaining links.

4.4 Operations

We’d like to consider the following operations. Where T is the type of object stored in the list.

void push_front(T value)
void pop_front()
Link* get_link(int i)
T& at(int i)
void push_back(T value)
void pop_back()
void insert(int index, T value)
void erase(int index)
size_t size()
iterator begin()
iterator end()

4.4.1 `push_front`

To insert an item at the front of the list, we simply create a new link with the relevant value and set its next pointer to the first item in the list. We then point the head at the new item.

Analysis: Regardless of how many items there are in the list (\(n\)), it will always take us \(1\) memory allocation, \(3\) pointer assignments and \(1\) pointer dereference to insert at the front of the list. We don’t care about these constants, we just care that it will always take the same amount of time, so we say that this operation takes constant time – \(O(1)\).

4.4.2 `pop_front`

To remove the item from the front of the list, we need to update the head to point to the next item and then delete the link that was originally at the front.

Note:

We need to make sure we still have a pointer to the item, otherwise, we would have a memory leak.
We can’t delete the item and then update head because after deleting the first item, we wouldn’t be able to access the next pointer. Again we would have a memory leak.

Analysis: Regardless of how many items there are in the list (\(n\)), it will always take us \(1\) memory deallocation, \(2\) pointer assignments and \(1\) pointer dereference to delete at the front of the list. We don’t care about these constants, we just care that it will always take the same amount of time, so we say that this operation takes constant time – \(O(1)\).

4.4.3 `get_link`

To get the link at index i, we need to traverse¹¹ to the correct link in the chain. This is like when you pick up a chain and move from link to link to link until you get to the one you want.

Analysis: In the worst case we traverse to the end of the list, in which case, we do \(n-1\) traversal steps (curr = curr->next). This is a linear function, so we say that we do \(O(n)\) operations.

Beware… get_link is a linear function, so the code below is not linear. What is the complexity of the following code segment?

LinkedList myList;
//... fill the list with items ...
for(int i = 0; i < n; ++i){
   Link *curr = myList.get_link(i);
   cout << curr->value << endl;
}

4.4.4 `at`

To get the value at index i, we need to traverse to the correct link and then return the value stored inside it. This is easy to implement because we already have a get_link function.

Analysis: The call to get_link is \(O(n)\) and then there is another \(1\) dereference operation. This results in a linear function plus a constant, which is still a linear function. So the complexity is still \(O(n)\) in the worst case.

4.4.5 `push_back`

To add to the back of the list, you need to traverse to the last link in the chain. You can do this with a while loop. Traverse until the curr->next == nullptr, which means that curr is pointing at the last link. Once you have a pointer to the last link, it is straightforward to allocate a new link and add it to the chain.

Analysis: For a list with \(n\) items, push_back will take O(n) operations. How could you alter the linked list data structure to achieve \(O(1)\) performance for this function?

4.4.6 `pop_back`

To remove the last item in the list, we need to update the next pointer in the link before the last one. This means that we should traverse to the second last link in the list, use its next pointer to deallocate the relevant memory, and then set the next link to the nullptr.

Analysis: For a list with \(n\) items, how many operations does it take to insert at the end of the list? Would your strategy to improve the performance of push_back work to improve the performance of pop_back? Why or why not?

4.4.7 `insert`

To insert at an arbitrary position, \(i\), in the list, we need to traverse to the link before \(i\), i.e. \(i-1\). We then create the new link and set its next pointer to point to the item currently at position \(i\). The next pointer at \(i-1\) should now point to the new link.

4.4.8 `erase`

To delete the value at an arbitrary position, \(i\), in the list, we need to traverse to the link before \(i\), i.e. \(i-1\). The next pointer at \(i-1\) needs to point to the link at \(i+1\). This removes the link from the list after that we free the memory for link \(i\). We need to be careful to store the address of the link that we’re deleting so that we can deallocate the memory – otherwise, we would have a memory leak.

4.4.9 Size

To get the size of the list we simply traverse from the front to the back counting the number of links until we reach the nullptr.

Analysis: In Big-Oh notation, how many operations will this function take? How can we alter the structure so that this happens in \(O(1)\)?

4.5 Iterators

4.5.1 What?

An iterator is an object that allows the programmer to traverse a container. Think of an iterator like a more sophisticated pointer. A C++ iterator¹² must provide two functions:

The dereference operator – T& operator*() – which returns a reference to the current object.
The increment operator – operator++() – which advances the iterator to the next object in the container.

In C++, all containers should have begin and end functions which return iterators. The begin function should return an iterator that references the first item in the container, while the end function should return a ‘one past the end’ iterator – this is an iterator that we would get if we called the increment operator one last time after hitting the last object. You should never dereference a one past the end iterator.

For vectors/arrays, pointers satisfy all the requirements of an iterator.

Thing* MyVector::begin(){
   return data;
}
Thing* MyVector::end(){
   return data+n_items;
}

The dereference (*) operator follows the pointer to the relevant object and because the objects are all contiguous, the increment (++) operator advances the pointer from object \(i\) to \(i+1\). Links in a linked list are not contiguous so this kind of pointer arithmetic will not work here. We need to build an iterator that acts in the same way, but knows that when incremented it should follow the next pointer in the link.

The iterator should store a pointer to a link in the list. The dereference operator should return a reference to the value in the link. The increment operator should advance our link pointer to the following link using next. For example:

class LinkedListIterator{
private:
   Link* pointer;
public:
   // Default constructor: The iterator contains a nullptr
   //   This represents a one-past-the-end iterator
   LinkedListIterator() : pointer(nullptr) {}
   // The iterator should store a link to the pointer provided
   LinkedListIterator(Link* p) : pointer(p) {}
   
   Thing& operator*(){
      return pointer->value;  // Return the relevant value
   }
   LinkedListIterator& operator++{
      pointer = pointer->next; // Traverse to the next link in the chain
      return *this; // We need to return a reference to this LinkedListIterator
   }
};

We can then write the begin() and end() functions for our LinkedList as follows:

LinkedListIterator LinkedList::begin(){
   return LinkedListIterator(head); // Pointer to the first link
}
LinkedListIterator LinkedList::end(){
   return LinkedListIterator();     // Pointer one past the last link (nullptr)
}

4.5.2 Why?

The obvious question is then: why do we care about iterators when we know how to access the items already? The answer is abstraction. By using iterators to traverse the container, it doesn’t matter what the underlying container is, the Standard Template Library (STL) is written so that many of the algorithms only need an iterator to function. This means that as long as your container provides the correct iterators, then you can use all the built-in algorithms that come with C++.

To manually iterate over a vector we could write:

for(int i = 0; i < myVector.size(); ++i){
   cout << myVector[i] << endl;
}

To manually iterate over a linked list we could write:

for(Link* curr = myList.head; 
    curr->next != nullptr; 
    curr = curr->next){
   
   cout << curr->value << endl;   
}

Both code segments above are correct and are equally efficient. However, the code for each looks really different. This is undesirable as it makes the code harder to read and harder to write. It means that we need to know the type of container before we can print the values. If we rewrite the loop in terms of iterators, then the same loop works for both types of container:

// auto tells the compiler to figure out what type the curr and end variables should be
// Thing* for MyVector / LinkedListIterator for LinkedList
for(auto curr = myContainer.begin(), end = myContainer.end();
    curr != end;
    ++curr){
   Thing& val = *curr; // Thing&
   
   cout << val << endl;   
}

We now have one for loop that can handle both types of container – if we decided to swap between Vectors or Linked Lists or any other containers we wouldn’t need to adjust our printing code. This pattern was so common that it was officially added into the language as range-based for loops¹³ which were introduced in C++11 and extended in C++20. The compiler will translate the range-based for loop below into the code above before compiling.

for(Thing& val : myContainer){
   cout << val << endl;   
}

4.6 Doubly Linked Lists

In the previous sections, we discussed ‘Singly Linked Lists’ which correspond to the forward_list<T> container in the STL.¹⁴ The links/nodes only contain pointers to the next item in the list and the list itself only contains a pointer to the head. There is no tail pointer and it does not keep track of its size.

If we would like to be able to access the last link in \(O(1)\) time, then we could also keep track of a tail pointer which we update whenever necessary. Consider how this affects the implementation and complexity of all the functions above. There is no container in STL that corresponds to a forward_list with a tail pointer.

In contrast to the ideas above, it might be useful to be able to traverse the container backwards as well. In this case, each link should store a next pointer as well as a prev pointer. These pointers allow us to traverse forwards and backwards respectively. This corresponds to the list<T> container in the STL.¹⁵ This structure stores both head (first link) and tail (last link) pointers as well as the number of links in the list.¹⁶

Consider how all of the functions and analysis in the previous sections would need to be adjusted for a doubly-linked list. Doubly linked lists will be examinable.

4.7 Other Linked List Structures

There are other types of linked lists, such as Circularly Linked Lists and skip lists as well.

A Circularly Linked List is a forward_list where the last link’s next pointer points to the first link.
A Circular Doubly Linked List is similar, except that there are both next and prev pointers. These are sometimes used when implementing certain types of Heaps, which we will study later on in this course.
A Skip List is a linked list where we can jump much further ahead in the list through an express lane. These structures are very clever and can give us \(O(logn)\) access times rather than linear time. Examining the complexity of a skip list involves probabilistic complexity analysis which you will learn in Honours.

4.8 Drawbacks of Linked Structures

4.8.1 Linear Searches

One of the significant drawbacks of a linked list is that you usually have to perform a linear search to get to the link that you want to access. Even worse, if you actually had a sorted list, you still wouldn’t be able to do a binary search because you would need to traverse to the centre node each time, which is \(O(n)\) and entirely defeats the point of the \(O(log n)\) binary search.

4.8.2 Locality of Reference – Caching

In modern computers, there is usually a small amount of cache memory on the CPU. When you access an item in memory, the cache remembers its value so that if you access it again, then the second call is faster – the number is already saved in the faster cache memory, so we don’t need to fetch it from RAM. This is called Temporal Locality.

When we have lots of data we usually place the data in contiguous blocks of memory (like in an array/vector) or in a class where the data members are usually next to each other. This means that if we access data at address \(i\) it is likely that we’ll access data at address \(i+1\). Because this is so common, the cache will load the content of neighbouring memory blocks when we ask for the content at \(i\). If we now ask for content at \(i+1\) it is already in the cache and the value is returned faster than if we had to fetch it from RAM. This is called Spatial Locality.

When we ask for a value, it is a cache hit if it is already in the cache. If it is not in the cache and we need to fetch it from RAM, then it is a cache miss. Because the memory is contiguous when using arrays, we usually have lots of cache hits. In practice, this means that arrays are often faster than linked lists even when you don’t expect them to be.¹⁷

4.8.3 Be Careful

In general, you should be aware that linked structures can be more inefficient than we expect, with traversals and caching/locality both playing a role. This translates into other languages as well, such as Lists in Java/Python/JavaScript etc. These structures have their place, but ensure that the actual behaviour of the structure on your hardware is as you expect.

Here is a great talk by the creator of C++, Bjarne Stroustrup, where he compares the run times of Vectors and Linked Lists with surprising results: https://www.youtube.com/watch?v=YQs6IC-vgmo

Here is a more recent video by Computerphile, where they run several experiments to investigate the efficiency of the different structures. https://www.youtube.com/watch?v=DyG9S9nAlUM

4.9 Lab

In the next lab, you need to implement your version of a forward_list along with additional copy and reverse functions. Relevant unit tests and function descriptions will be provided.

class Thing;

class Link{
public:
   Link *next = nullptr;
   Thing value;
};

class LinkedListIterator{
public:   
   Link* ptr = nullptr;
   
   Thing& operator*();
   LinkedListIterator& operator++();
};

class LinkedList{
public:
   Link* head = nullptr;
   
   LinkedList();
   ~LinkedList();
   
   void push_front(Thing t);
   void pop_front();
   
   void push_back(Thing t);
   void pop_back();
   
   size_t size();
   
   Thing& front();
   Thing& back();
   
   Link* get_link(int i);
   Thing& at(int i);
   
   LinkedListIterator begin();
   LinkedListIterator end();
   
   LinkedList* copy();
   void reverse();
};

4.10 Additional Reading

https://www.geeksforgeeks.org/data-structures/linked-list/
Chapter 3.2 (Singly Linked Lists), 3.3 (Doubly Linked Lists), 3.4 (Circularly Linked Lists & Reversals) – Goodrich, Tamassia, and Mount (2011)
Chapter 3.2, 3.3, 3.5 – Weiss (2014)
http://www.cplusplus.com/reference/forward_list/forward_list/
http://www.cplusplus.com/reference/list/list/

References

Goodrich, Michael T, Roberto Tamassia, and David M Mount. 2011. Data Structures and Algorithms in c++. 2nd ed. John Wiley & Sons.

Weiss, Mark A. 2014. Data Structures & Algorithm Analysis in c++. 4th ed. Pearson Education.

Recall that we discourage the use of compiler-specific extensions such as VLAs.↩︎
Contiguous memory is when all of the allocated blocks are next to each other/consecutive in memory. Similar to continuous, except we’re talking about discrete blocks.↩︎
Thanks to pointer arithmetic.↩︎
Like traversing terrain… NOT transverse. That is a type of wave.↩︎
http://www.cplusplus.com/reference/iterator/↩︎
https://en.cppreference.com/w/cpp/language/range-for ↩︎
http://www.cplusplus.com/reference/forward_list/forward_list/↩︎
http://www.cplusplus.com/reference/list/list ↩︎
Interestingly, storing the size was only required in C++11. In C++98 the complexity requirement of the size function was ‘up to linear’. This means that the compilers could implement it using either approach. When the complexity requirements became \(O(1)\) in C++11, the compilers were forced to keep track of the size.↩︎
Remember that we noted earlier that \(O(\cdot)\) hides the constants associated with the different operations, but also assumes that the operations themselves take the same amount of time – e.g. assignment always takes the same amount of time. Caching breaks this assumption and in some cases, the memory access patterns may be more important than we’d otherwise think.↩︎