Chapter 6 Stacks
6.1 Introduction
Often we would like to keep track of objects or events in a way that allows us to access the newest/most recent one first. For example, we have seen the Call Stack which keeps track of functions and makes sure that the functions are always ordered from the most recent call (i.e. the function that we’re currently in) to the oldest call (i.e. the main function). When we call a new function, its stack frame (memory for automatic variables, program counter/line number etc.) gets added to this structure and when the function returns, then that frame is removed from the structure. We are always working on the same end of the structure: adding and removing items that are the most recent. This type of structure follows a Last In First Out (LIFO) structure,19 because the last thing that we added, is the first one that can be removed. This type of structure is called a Stack and is illustrated in Figure 6.1.

Figure 6.1: A Stack of Pancakes
When a new pancake has been cooked we always place the new pancake on top of the stack. When we remove a pancake,20 we always remove the pancake which is on top – this means that the pancake we remove is always the one that was cooked most recently. The last pancake placed onto the stack is the first pancake we remove from the stack and devour. Beyond this, we can add and remove pancakes arbitrarily: you’re cooking, I’m eating… You place p1 onto the stack [p1], then you place p2 onto the stack [p1, p2], then you turn around and I remove p2 and eat it [p1], you come back and place p3 onto the stack [p1, p3], then you place p4 onto the stack [p1, p3, p4], then you place p5 onto the stack [p1, p3, p4, p5], then I eat p5 [p1, p3, p4], then p4 [p1, p3], then p3 [p1]… Then you eat p1, which is probably cold by now anyway.
Stacks are very useful structures whenever we want to be able to retrace our last steps. Think of the undo button in any computer program. As you perform different operations, the program stores each action on a stack. The most recent thing that you did is on top of the stack and the most recent thing after that is underneath it. If you hit undo, it will remove the last action that you did from the top of the stack and do the opposite action. If you hit undo again, it will remove the second last action from the stack and reverse that action. As you perform an action it is added to the top of the stack, as you hit undo, the action on top of the stack is removed and then reversed in the program. Go to your favourite word processor and play around with the undo button. Think about what the stack would look like at each point.
There are plenty of other examples of stacks that you use every day. Think about how the examples below form a stack and how objects would be added or removed.
- The back button in your browser.
- The forward button in your browser. When do pages get added to this stack?
- Views/activities/pages in a mobile application (imagine navigating forward and backwards through the settings page of an app).
- Recursive function calls in a C++ program.
- Retracing your steps after hitting a dead-end in a maze.
You can see in the examples above, we often use stacks to keep track of decisions that we have made, and then use the stack to retrace our steps if we decide that we have made a mistake. This is how we can implement a class of algorithms called backtracking algorithms. You came across this idea previously in IAP when you discussed how to solve a Sudoku by using a recursive function. That algorithm used the call stack to keep track of your actions when you realised you’d made a mistake, the function returned false and the previous function resumed after undoing the changes you’d made – Figure 6.2. Later on in this chapter, we’re doing to talk about how to implement a backtracking algorithm without recursion, by managing the stack ourselves.
There are lots of other problems that can be solved with backtracking algorithms. Some of these are discussed further here https://www.geeksforgeeks.org/backtracking-algorithms/.
Before we move on to how we can use stacks, let’s first talk about the interface of the Stack ADT (Section 6.2) followed by some implementations (Section 6.3).
6.2 Operations
A Stack is a fairly simple ADT. It has only 4 important functions. Note that there is no operator[] or at function because we are only ever allowed to access the item on top of the stack. The only way to access other items would be to pop off items until the one we wanted was at the top. In general, if you need “random access” to access arbitrary items in the container, then a stack is probably the wrong data structure and you should consider using something else.
Assume that T is the type of object stored in the list, e.g. int.
void push(T value)- Add value to the top of the stack.
void pop()- Remove the item from the top of the stack.
T& top()or sometimesT& peek()- Return a reference to the top item.
size_t size()- Return the number of items in the stack.
6.3 Implementations
There are two main implementations for a stack, one is based on contiguous memory, the other is based on a linked list.
6.4 std::stack<T, C>
The C++ Standard Template Library provides the std::stack template class – http://www.cplusplus.com/reference/stack/stack/. This class uses an underlying container such as a vector or list but can use any container that provides the empty, size, back, push_back and pop_back functions. By default it uses a double-ended queue (deque) as the underlying container – we’ll discuss this structure later on in the course – this is a sensible default and is usually the right choice.
You can create a std::stack in the following ways:
#include <stack>
using std::stack;
class Thing;
// Stack of Things, underlying container: deque<Thing>
stack<Thing> s0;
// Stack of Things, underlying container: deque<Thing>
stack<Thing, deque<Thing>> s1;
// Stack of Things, underlying container: vector<Thing>
stack<Thing, vector<Thing>> s2;
// Stack of Things, underlying container: list<Thing>
stack<Thing, list<Thing>> s3;6.5 Applications
6.5.1 Postfix Notation
When we’re doing arithmetic, we use infix notation to represent the operators and operands of a formula. This means that the operator (+ - x ÷) acts on the operands which are on either side of it – the operator is in the middle, e.g. a + b.
In the 1920s a Polish mathematician, Jan Łukasiewicz, invented Polish Notation. He showed that by writing the operators in front of the operands you no longer need brackets to disambiguate the order of operations, e.g. + a b. Reverse Polish Notation (RPN) was then proposed by Philosopher and Computer Scientist, Charles Hamblin. In this approach, the operators come after the operands. The benefit of this is that the operators all appear in the order that they will be evaluated. This approach is also called postfix notation because the operators are after the operands, e.g. a b +.
RPN was used in the instruction language of the English Electric computers in the 1960s. Hewlett-Packard engineers found that by requiring the user to enter instructions in RPN, the electronics inside their early calculators could be dramatically simplified. This means that users needed to learn the new notation, but that the number of components in and therefore the cost of the calculators could be reduced. In 1968, the HP9100A became the first calculator to use RPN and is widely considered to be the first desktop computer.
By using RPN, the machine does not need to parse the formula first and intermediate values do not need to be written down as brackets are completely unnecessary. These days, machines are powerful enough that parsing or understanding the infix formulae does not cost much computational time. Similarly, transistors are so small and cheap, the extra hardware required to do this does not affect the price or size.
Several modern calculators like the HP12C still use this notation and if you take the Wits Actuarial Science course you are likely using one!
To evaluate a postfix expression, we perform the following algorithm and make use of a stack to store the intermediate results which form the operands. When we read a number, we push it to the stack, when we read an operator we pop as many operands as are required, perform the operation, and then push the result back onto the stack.
OUTPUT: Evaluation of the expression
Initialise empty stack s
for each token in the postfix expression:
if token is a number:
push it to the stack
else if is an operator:
pop k numbers off of the stack
perform the operation
push the result back onto the stack
There should be 1 number remaining on the stack
RETURN this number as the result of the expression
There is a straightforward algorithm that also uses a stack, to convert an infix formula into a postfix one. If you were building your own calculator, you could accept an infix expression (10+5*2), convert it into a postfix expression (10 5 2 * +) and then evaluate it using the postfix algorithm above.
This technique is used extensively by compilers as they convert your source code into machine code.
6.5.2 Depth First Search
Searching through a Maze
We mentioned earlier that Stacks are often used when we need to retrace our steps or backtrack. When we have a search space (e.g. a maze), we can perform a systematic search of the maze by doing a Depth First Search. This means that we make a decision about which direction to take at the first junction and then try every path from there. If we hit a dead end, we go back to the last decision we made and change it. The idea here is that we go deep down a path until we’re forced to turn back. 21
Solving Sudoku
THe kind of search explained above does not always have to happen in a maze or other ‘physical space’. We can think of each position in a search space corresponding to a different state of the world as well. In the maze above, each decision was one of four directions. When solving sudoku, each decision involves setting the value of a cell to one of nine numbers. In the maze, we followed a path until we hit a dead end and couldn’t make any valid turns. When solving a sudoku, we can make a decision (i.e. place a number in an empty block) and then check if the state of the board is valid. If so, then we can make that move and try all boards that lead on from that state. If none of those boards are solvable, then we must have made an incorrect move and we need to change that decision (i.e. that number needs to be updated to a different number).
At each decision, we push our action onto the stack. If we later realise that there are no valid boards from this decision onwards (i.e. we made a decision that leads us to a dead-end), then we can pop that action off the stack, try the next action, and then check those boards.
We will formalise this algorithm below, where we consider your first project.
In IAP you saw this code when learning about recursion:
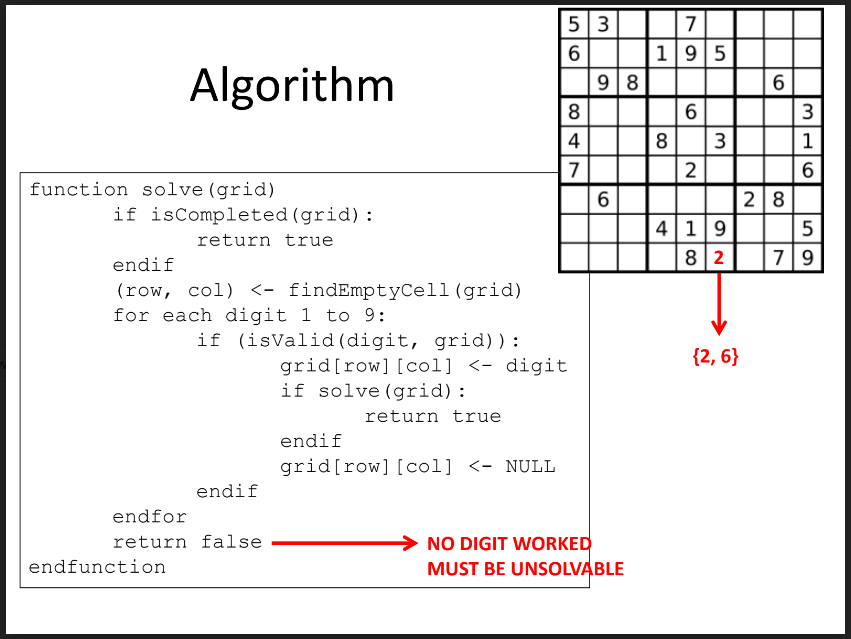
Figure 6.2: Sudoku Pseudocode from IAP
This code is doing the same thing! This code is a recursive implementation of a Depth First Search. It uses the call stack to keep track of decisions and, as each function returns, the previous state of the sudoku can be restored.
6.6 Lab
You need to implement both types of stack: based on a vector and based on a linked list.
Here is the interface for a stack:
class Thing;
class Stack{
public:
// Add t to the top of the stack
void push(Thing &t);
// Remove the top item from the stack
void pop();
// Return a reference to the top item in the stack
Thing& top();
// Return the number of items in the stack
size_t size() const;
// Return true/false based on whether the stack is empty
bool empty() const;
public:
vector<Thing> data; // list<Thing> data;
};You should make use of the relevant functions from the vector (vector<Thing>) and linked list (list<Thing>) structures from the Standard Template Library (STL). Both implementations should look remarkably similar.
6.7 Project: Solving Sudokus
You need to write a sudoku solver using a Depth First Search. Your code must output the correct solution for a given input. The size of the sudoku will vary (\(4\times 4\), \(9 \times 9\), \(16\times 16\), \(25\times 25\)). Part of your grade in this project will be competitive – based on the amount of time it takes your submission to solve an \(n\times n\) sudoku and how well it scales.
The grading scheme and due dates will be available via the formal project brief on Moodle.
6.8 Additional Reading
- https://www.geeksforgeeks.org/stack-data-structure/
- Chapter 5.1 (Stacks) – Goodrich, Tamassia, and Mount (2011)
- Chapter 3.6 – Weiss (2014)
- Chapter 5.1 and 5.2 – Dale, Weems, and Richards (2018)
- http://www.cplusplus.com/reference/stack/stack/
- https://ocw.mit.edu/courses/civil-and-environmental-engineering/1-00-introduction-to-computers-and-engineering-problem-solving-spring-2012/lecture-notes/MIT1_00S12_Lec_35.pdf
- https://www.geeksforgeeks.org/backtracking-algorithms/