6 Queues

6.1 Introduction

In the previous chapter, we discussed the idea of a stack that allowed us to access the most recent item. This enables us to implement a class of algorithms called backtracking algorithms because to undo the most recent action, we could check the top of the stack. In many algorithms, we need to do a similar operation, but we need to access the first item that was added, i.e. the one that arrived first. This type of structure forms a Queue. Just like every queue you’ve ever stood in, we add to the back and remove from the front. A queue is known as a First In First Out (FIFO) structure.

We often use queues when we need to process objects in the order that they arrive. For example, when you are typing on the keyboard the hardware generates a keypress event which stores which key was pressed. The operating system gets notified of the event through an interrupt and it adds it to an event queue for our program to process. When our program is running, we can ask the OS to give us each event to process. The events must be given to us in the same order that they were generated, otherwise, we’d receive mixed up data.

Figure 6.1: Pizza queue at Zesty Lemonz during lunch.

This is such a common process that when writing games we often create an event loop that looks something like the code below.²¹ In the code below, the operating system will add SDL_Event objects to the event queue. When we call SDL_PollEvent it will check whether there is an event in the queue, if there is, it will remove it from the front and place it into e. We can then check what type of event it is and update the state of our game (e.g. change the position of the character). Once we have handled the event, our loop repeats and we check whether there is anything else in the event queue. if there is nothing in the queue, then we update the state of our game (e.g. did the character collect treasure in this move?) and redraw the updated image to the screen. Then our main loop repeats and we check for more input events from the user.

while(!quit){
  // This object contains the event information
  SDL_Event e;               
  
  // Ask for an event from the queue
  // While there are events, remove from the queue and process
  while(SDL_PollEvent(&e)){   
    if(e.type == SDL_QUIT){   
      // If the window was closed
      quit = true;
    }else if(e.type == SDL_KeyboardEvent){ 
      // Handle a keyboard button
      handle_keyboard_event(e);
    }else if(e.type == SDL_MouseButtonEvent){ 
      // Handle a mouse button
      handle_mouse_event(e);
    }
  }
  
  // Update the game state.
  update_state();
  // Draw to screen.
  draw();
  // Repeat
}

In the example above, the operating system added events to the back of the queue and our program removed events from the front. With a stack, we could only ever access the item at the top. With a queue, we can only ever access the item at the front. If you need to access another item in the container, then you’re using the wrong structure.

Whenever you want to process data in the order that it arrives, then a queue is the correct data structure to use. Some examples of queues include:

Event Queues.
Print Queues.
Wits in-person registration queues.
Asking Richard questions during tutorials.
A Breadth-First Search – Section 6.5

Again, just as with the stack, we can implement it using linear data structures that we have already built: vectors and lists. Although we’ll see that using vectors directly leads us to an inefficient implementation and in this case if we want to use contiguous memory, then we should implement something new called a Circular Array.

6.2 Operations

A Queue is a very simple ADT. It has only 4 important functions. Note that there is no operator[] or at function because we are only ever allowed to access the item at the front of the queue. The only way to access other items would be to dequeue/pop off items until the one we wanted was at the front – except then we wouldn’t be able to replace those items at the front as we can only add at the back. In general, if you need “random access” to access arbitrary items in the container, then a queue is probably the wrong data structure and you should consider using something else.

Assume that T is the type of object stored in the queue, e.g. int.

void push(T value) or void enqueue(T value)
- Add value to the back of the queue.
void pop() or void dequeue()
- Remove the item from the front of the queue.
T& peek() or T& front()
- Return a reference to the front item.
size_t size()
- Return the number of items in the queue.

6.3 Implementations

We will consider two implementations of a queue, one is based on contiguous memory, the other is based on a linked list.

6.3.1 Contiguous Implementation

6.3.2 Linked List Implementation

6.4 `std::queue<T, C>`

The C++ Standard Template Library provides the std::queue template class – http://www.cplusplus.com/reference/queue/queue/. This class uses an underlying container such as a deque or list but can use any container that provides the empty, size, front, back, push_back and pop_front functions. By default it uses a double-ended queue (deque) as the underlying container. This is a sensible default and is usually the right choice as a deque contains pop_front and push_back functions that are both \(O(1)\) time.

You can create a std::queue in the following ways:

#include <queue>

using std::queue;
class Thing;

//Good:
// Queue of Things, underlying container: deque<Thing>
queue<Thing> q0;
// Queue of Things, underlying container: deque<Thing>
queue<Thing, deque<Thing>> q1;
// Queue of Things, underlying container: list<Thing>
queue<Thing, list<Thing>> q2;

//Bad:
// Queue of Things, underlying container: vector<Thing>
//   This is a compile error because vector does not have a pop_front
queue<Thing, vector<Thing>> q3;
// Queue of Things, underlying container: forward_list<Thing>
//   This is a compile error because forward_list does not have a push_back
queue<Thing, forward_list<Thing>> q4;

6.5 Project – The Shortest Path in a Maze (BFS)

6.5.1 Breadth First Search (BFS)

The problem of finding the shortest path occurs frequently in applications such as computer games, satellite navigation, and network routing. For GPS maps with routing such as Waze and Google Maps, this is their primary function. These systems work on a structure called a graph, which you’ll learn more about later in COMS2.

In this project, you will need to calculate a path through a maze using a Breadth-First Search. This will be useful on the snake game for example, where you may need to find the shortest path from the head of a snake to the apple so that you can get there first. Another example is if you were implementing Artificial Intelligence for the ghosts in Pacman. In this case, the source may be the ghost’s current position, and the goal would be Pacman’s current position.²² You will implement the BFS algorithm in a new program that will be submitted to Moodle for automatic marking.

6.5.2 Algorithm

Because each step in the path towards the goal costs the same (uses the same amount of energy/takes the same amount of time/etc), we can use a standard breadth-first search to find the shortest path. The first path found that starts at the source and ends at the goal will be the shortest path.²³ Starting at the source, the algorithm proceeds as follows:

Starting at the source, find all new cells that are reachable at distance 1, i.e. all paths that are just 1 unit in length, and mark them with that length.
Using the distance 1 cells, find all new cells which are reachable at distance 2.
Using all cells at distance 2 from the source, find all cells with distance 3.
Repeat until the target is found. This expansion creates a wavefront of paths that search broadly from the source cell until the target cell is hit.
From the target cell, select the shortest path back to the source and mark the cells along the path.

This ‘wavefront’ is called the fringe – the edge of what we’ve seen so far. At each iteration, we take a cell from the fringe and look at its undiscovered neighbours. Note that if it takes \(n\) steps to get to an item in the fringe, it then takes \(n+1\) steps to get to any of its undiscovered neighbours. By checking all paths of length \(n\) first, we can be sure that there is no quicker way to get to an undiscovered neighbour.²⁴ The fringe can be represented using a queue, this means that in iteration \(i\), dequeue a cell from the fringe and enqueue all of its unvisited neighbours, which will have a path length of \(i+1\). Because the fringe is FIFO, we will dequeue all cells at level \(i\) before we dequeue any cells at level \(i + 1\). It turns out that this is a simplified, special case of Dijkstra’s algorithm for finding the shortest path in a graph. You’ll learn more about this next year.

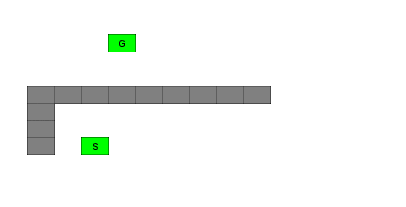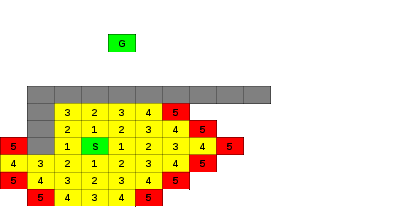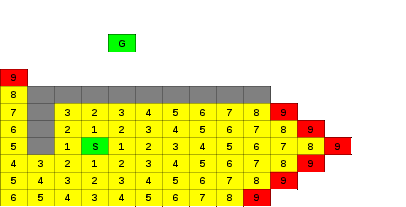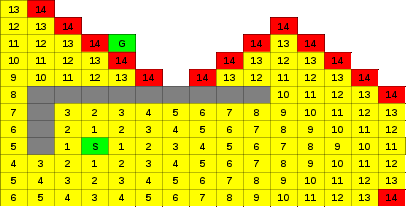
Figure 6.2: BFS Wavefront

6.5.3 Examples

The figures below show how the wavefront propagates through the maze and around obstacles. The red blocks indicate the cells in the fringe (wavefront). The green blocks indicate the start and endpoints. The numbers show how many steps we must make to get from the start point to the relevant block.

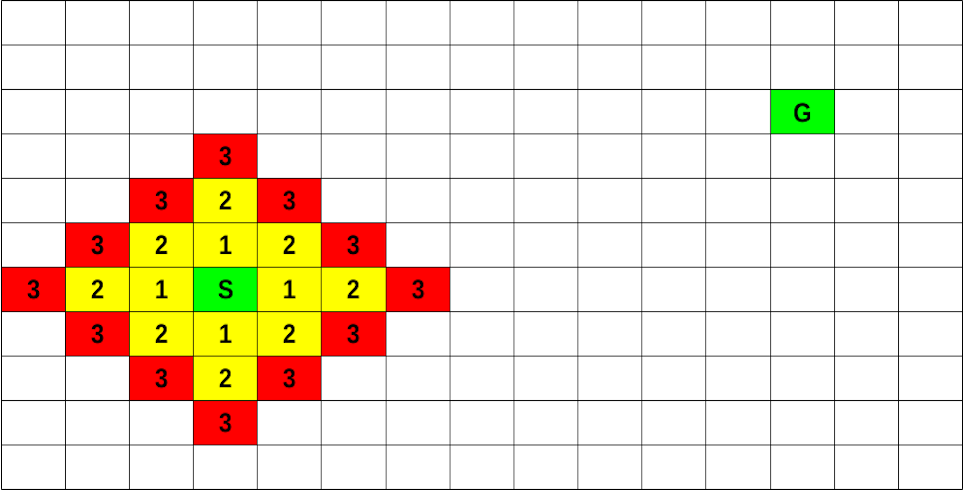
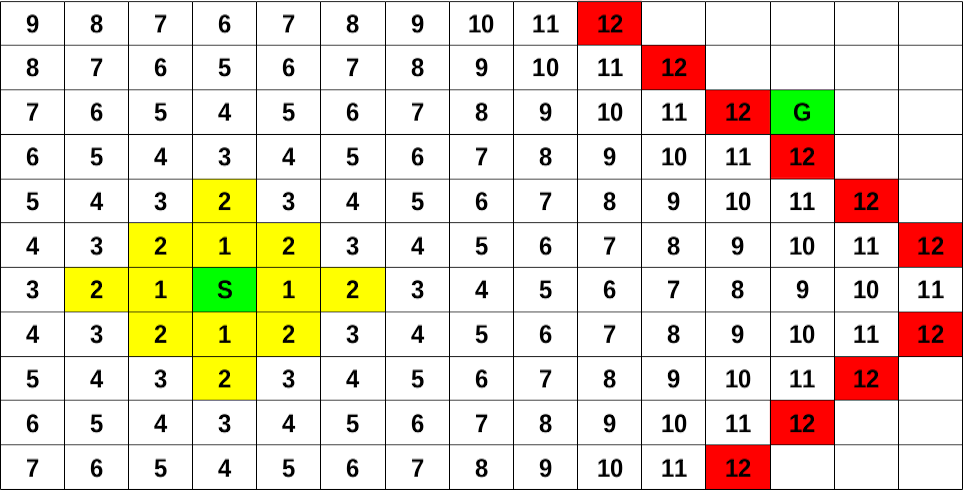
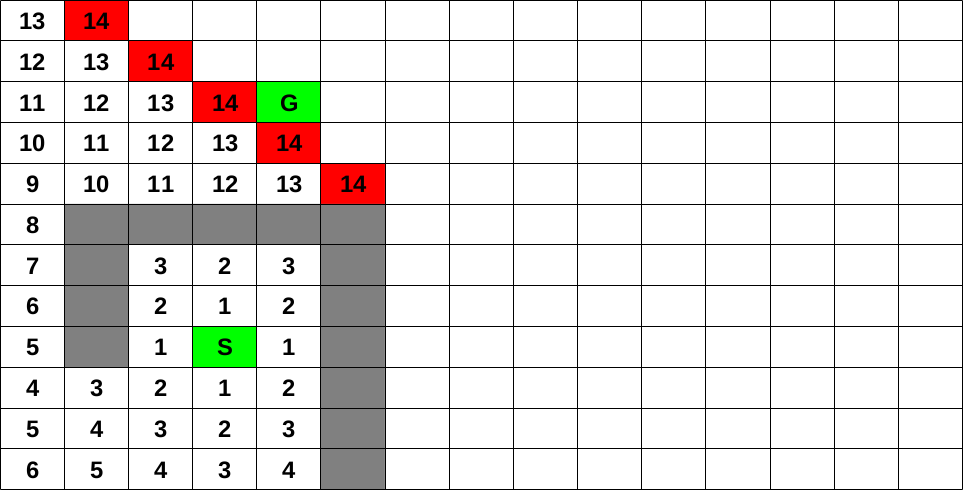
Figure 6.3: BFS Examples

6.5.4 Pseudocode

When running on a grid where each step costs the same, the shortest path algorithm reduces to a normal breadth-first search. In the algorithm that follows, we make use of a queue to keep track of the fringe. We use a parent array to keep track of the row/column indices of the cell through which we travelled on the way to the current cell. The distance array keeps track of how long the path is to get from the source to the current cell. When we have found a path to the goal, we follow the parent array back to the source and reverse it to get the shortest path from the source to the goal.

Figure 6.4: BFS Examples

Note: While it doesn’t affect the correctness of your algorithm in general, for the marker it is important to visit neighbours of the current cell in the correct order: down, left, up, right.

6.5.5 Sample Input/Output

You will receive the following input format on stdin:

The first line will contain 2 integers, m and n, separated by a space. These numbers represent the number of rows and columns in the grid respectively.
There will then be m lines each with n columns that represent the maze.
- A space represents an open block in the world. You may travel through this block.
- An x represents an obstacle. You may not travel through this block.
- An S represents the start.
- A G represents the goal.
The output should be the maze with * characters along the shortest path from the start to the goal. 1 If there is no path between the start and goal, then the output should say No Path.

maze1.txt            maze2.txt            maze3.txt
14 17                14 17                14 17
xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx
x               x    x      x        x    x      x        x
x               x    x xxxx   x      x    x xxxx   x      x
x            S  x    x    xxxxx   S  x    x    xxxxx   S  x
x               x    x      x   xxxx x    x      x   xxxx x
x               x    x  xxx xxxxx    x    x  xxx xxxxx    x
x               x    xxxxxx     x xxxx    xxxxxx     x xxxx
x               x    x          x    x    x          x    x
x  xxxxxxxxx    x    x  xxxxxxxxxxxx x    xxxxxxxxxxxxxxx x
x          x    x    x          x    x    x  x       x    x
x  x xxxx  x    x    x Gx xxxx  x xxxx      Gx xxxx  x xxxx
x  x      Gx    x    x  x       x    x       x       x    x
x  x            x    x  x            x       x            x
xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx

Output1:             Output2:             Output3:
xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx    No Path
x               x    x******x***     x
x               x    x*xxxx***x*     x
x            S  x    x*   xxxxx***S  x
x            *  x    x******x   xxxx x
x            *  x    x  xxx*xxxxx    x
x            *  x    xxxxxx*    x xxxx
x            *  x    x *****    x    x
x  xxxxxxxxx *  x    x *xxxxxxxxxxxx x
x          x *  x    x *        x    x
x  x xxxx  x *  x    x Gx xxxx  x xxxx
x  x      Gx *  x    x  x       x    x
x  x      ****  x    x  x            x
xxxxxxxxxxxxxxxxx    xxxxxxxxxxxxxxxxx

6.5.6 Submission & Grading

Submit a single cpp file to Moodle. Moodle will attempt to compile and run your file with the following command:

g++ -g -std=c++23 source.cpp -o bfs
./bfs < maze.txt

You may use any built-in C++23 STL types that you think are useful. Depending on your compiler version, you migh need to use the -std=c++2b flag to activate C++23.

There are many test cases on Moodle that handle various mazes with and without valid paths and that will test several edge cases in your code.

6.6 Additional Reading

https://www.geeksforgeeks.org/queue-data-structure/
Chapter 5.2 (Queues) – Goodrich, Tamassia, and Mount (2011)
Chapter 5.3 (Double-Ended Queues) – Goodrich, Tamassia, and Mount (2011)
Chapter 3.7 – Weiss (2014)
Chapter 5.3 and 5.4 – Dale, Weems, and Richards (2018)
http://www.cplusplus.com/reference/queue/queue/
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-006-introduction-to-algorithms-fall-2011/lecture-videos/lecture-13-breadth-first-search-bfs/ or https://www.youtube.com/watch?v=s-CYnVz-uh4
https://towardsdatascience.com/graph-theory-bfs-shortest-path-problem-on-a-grid-1437d5cb4023
https://medium.com/analytics-vidhya/part-i-breadth-first-search-using-grid-dc41a5f41663

References

Dale, Nell B, Chip Weems, and Tim Richards. 2018. C++ Plus Data Structures. 6th ed. Jones & Bartlett Learning.

Goodrich, Michael T, Roberto Tamassia, and David M Mount. 2011. Data Structures and Algorithms in c++. 2nd ed. John Wiley & Sons.

Weiss, Mark A. 2014. Data Structures & Algorithm Analysis in c++. 4th ed. Pearson Education.

This is based on the SDL framework. If you’re using a high-level framework like Unity or a language like Java, then the event loop and dispatch will usually be done automatically for you.↩︎
Technically, in Pacman the ghosts (Blinky, Pinky, Inky and Clyde) have different goals. Blinky aims directly at Pacman, Pinky aims two blocks ahead of Pacman, Inky aims 2 blocks ahead of Pacman but with the distance doubled based on the distance between the ghost and Pacman. Finally, Clyde will chase Pacman just like Blinky, unless he is fewer than 8 tiles away, in which case Clyde will retreat to the bottom left corner of the map. In each case, a BFS could be used to find the shortest path to the goal.↩︎
This would not be the case if different steps cost different amounts. In that case, you’d need to use a priority queue in the BFS, which leads you to an implementation of Dijkstra’s algorithm. You will be doing this next year.↩︎
See if you can prove this, try a proof by induction and/or contradiction.↩︎