Chapter 6 Functions
Up to this point, we’ve written our programs as a sequence of
instructions, one after the other. We might say that the code we’ve
written is one big monolithic block. It gets the job done, but that’s
about it — it can’t be reused or repurposed by anyone else. However,
we have (perhaps unknowingly) been using other people’s code in our own
programs. For example, if at any point you computed the square root of a
number, you used someone else’s code to do it! Some programmer had
written functionality for computing the square root of a number and
placed it in Python’s math library. In doing so, it made it very easy
for us to just use it, like so:
import math
x = 5
print(math.sqrt(x))In this chapter, we will look at the concepts of functions, why we need them and how to create our own ones.
6.1 Motivation
In the above code, sqrt is a Python function that someone else has
written for us to use. To motivate why this is useful, let’s consider
what would happen if no such function existed, and we had to do it
ourselves. If we were to write a program to compute the square root of a
given number, it might look something like this:
n = float(input())
x = n
tolerance = 0.0000000001 # allowed error
while True:
root = 0.5 * (x + (n / x))
if abs(root - x) < tolerance:
break
x = root
print(root)Numerics side quest! The code above uses the Newton-Raphson method to compute the square root in a loop. However, there is a famous piece of code for computing the inverse square root without any loops that uses the hexadecimal number 5f3759df. Find out more about this magic number by researching the fast inverse square root.
The above code will compute the square root of a given number within some error, which is great! But there’s a problem: every single time we need to compute the square root, we would need to rewrite this code! Who has time for that?! Even worse, image we were asked to calculate the sum of two square roots! Then we would have to duplicate the code as follows:
n = float(input())
x = n
tolerance = 0.0000000001 # allowed error
while True:
root = 0.5 * (x + (n / x))
if abs(root - x) < tolerance:
break
x = root
n2 = float(input())
x2 = n2
while True:
root2 = 0.5 * (x2 + (n2 / x2))
if abs(root2 - x2) < tolerance:
break
x2 = root2
print(root + root2)So now we’re really wasting our time!
Instead, the obvious thing to do is to write the code exactly once,
package it up somewhere, and then simply reuse the code as and when we
need it. Since we have the sqrt function provided to us by Python’s
math library, the above code can simply be written as:
import math
n = float(input())
n2 = float(input())
print(math.sqrt(n) + math.sqrt(n2))So much easier!
6.2 What are Functions?
Depending on the language you’re using, functions may also be called
methods, procedures or subroutines. Whatever their names, functions are
essentially pieces of code that have been “packaged” as a single unit.
They usually serve a single purpose or complete a single task, such as
the sqrt function we just looked at. And just like the functions we’ve
been using so far, we can call a function as many times as we want.
Ultimately, functions are essentially identical to the concept of mathematical function which you’ll be familiar with. For example, let’s consider the simple case \(f(x) = x^2\). This is a function with the following properties:
- The name of the function is \(f\). This name is completely arbitrary, and could be anything we wanted. We could call our function \(blah\), and it wouldn’t change anything: \(blah(x) = x^2\)
- The function takes a single parameter \(x\). Again, \(x\) is an arbitrary name. If we were modelling something to do with time, perhaps \(t\) would be a better variable name: \(f(t) = t^2\).
- Functions can also take multiple parameters. For example, we could have \(g(x, t) = x^2t\), which takes in two parameters.
- We can call or invoke a mathematical function by providing it with an argument. For example, \(f(2)\) is the case of us providing the argument \(2\) to function \(f\), which will obviously produce \(2^2\). Similarly, we could say \(g(1,2)\) which provides two arguments to \(g\) and produces an answer of \(2\).
Of course, if we wish to create a Python function, we must follow Python syntax rules. Below, we see how the function \(f\) above is translated into a Python function that is functionally identical.
6.3 Defining Python Functions
In Python, functions take the following form:
def <function_name>(<parameter_list>):
<function_body>Let’s analyse each of these components in turn.
First, we have
def. This is a Python keyword that lets the interpreter know that we are defining a function. All functions must start with this keyword.Next we have the function name. This is how we will refer to the function, and follows the same naming conventions as regular variables. We can assign a function any name that we want, but it should be as descriptive as possible. Note also that we are not allowed to define two functions with the same name. Each function should therefore be given its own name.
In round brackets, we have the parameter list. These indicate the variables that the function accepts as input. As we will see in the examples below, we can have as many or as few parameters as we want. We can even have zero parameters, in which case we simply leave the parameter list blank (but we must always have the round brackets). The parameters are simply variables that will be used by the function, and we can given them any name we wish.
Next is the colon. Just like if statements and loops, in Python the colon indicates that the indented lines below are associated with the function.
The function body are the lines of code that should be executed when we use the function. Just as before, the body is defined with indentation.
A Python function may also end in a return statement (but this is
optional), the general form of which is given below.
def <function_name>(<parameter_list>):
<function_body>
return <exp>The return statement specifies the output of the function — that is,
it specifies the result of the computation performed by the function
(<exp> is simply a Python expression). It is very important to note
that the output of a function is NOT the same as print. When we
print, we are simply displaying something on the screen for a human to
read. On the other hand, the value that is returned (or output) by a
function is its result, which can be stored in a variable, or itself
printed out if need be. For example, when we use the sqrt function,
the answer produced by that function is returned by the function. The
answer can the be stored in a variable or printed out, as below:
import math
x = math.sqrt(4) # inside the sqrt function, the value is returned and assigned to x hereLet’s look at a few examples below to make things clearer
# a function called add that accepts two parameters and adds them up
def add(x ,y):
return x + y
# a function that has no parameters
def greet():
print("Hello") # this function does not return. Printing to the screen is not returning!
# A function that accepts a string and integer as parameters
def greet2(name, num_times):
for i in range(num_times):
print("Hello", name)6.4 Invoking Python Functions
Having defined the above functions, the next question is how to use them? Making use of a function is known as calling or invoking it and is done by using the function name and passing arguments to the function (if it has any parameters). The examples below show how to invoke the functions we just defined:
# remember that add takes two parameters
x = 5
y = add(2, x) # the returned value is stored in y
# greet takes no parameters
greet()
# greet2 takes 2 parameters
greet("Bob", 10)Note that we can pass variables or constants to our functions, but the
number of arguments we send in must match the number of parameters. For
example, we cannot say add(1) because the add function expects two
parameters, not one!
One important aspect of using functions is that, just like variables, functions must be defined before they are used. Let’s consider the following example:
m = int(input())
n = int(input())
show_message(m, n)
def show_message(x, y):
for i in range(x):
for j in range(y):
print("*", end="")
print()If we try run this code, we will receive the error message below.
NameError: name 'show_message' is not definedThis is because we have tried to use the show_message function on line
3, but the function itself was only declared afterwards. And since
Python will process code line by line, it does not yet know of its
existence!
To fix the problem, we must simply define the function before we use it, as follows:
def show_message(x, y):
for i in range(x):
for j in range(y):
print("*", end="")
print()
m = int(input())
n = int(input())
show_message(m, n)We may define functions anywhere before we use it in our code. They may
exist in the same file, but we could also put functions in different
files. In this case, we must import the functions so that we can use
them. This is why we often write import math. We wish to use the
function that are defined in the math file on our system.
Python side question! Try locate the math file somewhere on your
system and examine it. What’s with the funky code? Hint: it’s not
actually a Python file.
6.5 Function Returns
When a function finishes executing its code, the function returns control to the line where it was invoked. In other words, after the function has performed the task, the program will continue execution from the point after the call
When a function terminates, it is said to return. There are three ways that a function can terminate:
- If it executes all the statements in its body.
- If it runs into the statement
return. - If it runs into the statement
return <exp>, where<exp>is a Python expression.
If a function does not return a value or variable (as in the first two cases), it is said to be a void function. Otherwise, it is a non-void function.
Question! Earlier on, we defined three functions. Classify each of them as void or non-void.
Let’s look at examples of each of these:
# we run into the end of the function and exit
def f():
print("Hello, world!")
# returns here
# early return from void function
def g(x, y):
if y == 0:
print("y can't be 0")
return # returns here
print("Calculating...")
z = (x * x + y * y) / y
print("The answer is", z)
# return from non-void
def h(firstName, surname):
f() # functions can invoke other functions!!
if firstName == "" or surname == "":
return "Default Name" # returns here
return firstName + " " + surname # returns here
So what exactly can Python function return? In languages like C++ or Java, we are only allowed to return one thing. But in Python, we can return as many values as we want (hurray for Python!). However, it is good practice to return one logical thing, because we don’t want our function doing too much work. If our function is returning too many things, it’s often a good indication that we should split it into two functions instead. An example of a good function that returns multiple things (but one logical thing) is below:
def get_position_of_robot():
# get the xy position of a robot
# ... do calculations
x = ...
y = ...
return x, yFinally, it is important to note that once the function returns, the variables in the parameter list and any other variables that it declares are lost.
6.6 Function Properties
Functions embody two of the most important principles in computer
science: interfaces and encapsulation/abstraction. Again consider
the sqrt function that Python provides. How exactly does it work? The
answer is: it doesn’t matter at all to us! We don’t care at all about
how it works — all we care about is that we can give it a number, and
it will give us back the square root. This is the idea behind
encapsulation — the complexity of the function is hidden from us. All
we know is its interface (we give it a number, it gives us back another
number). One great thing about this concept is that, if someone decided
to write a better, faster sqrt function, they could go ahead and
replace the code, and it wouldn’t affect us at all! The diagram below
encapsulates this idea:
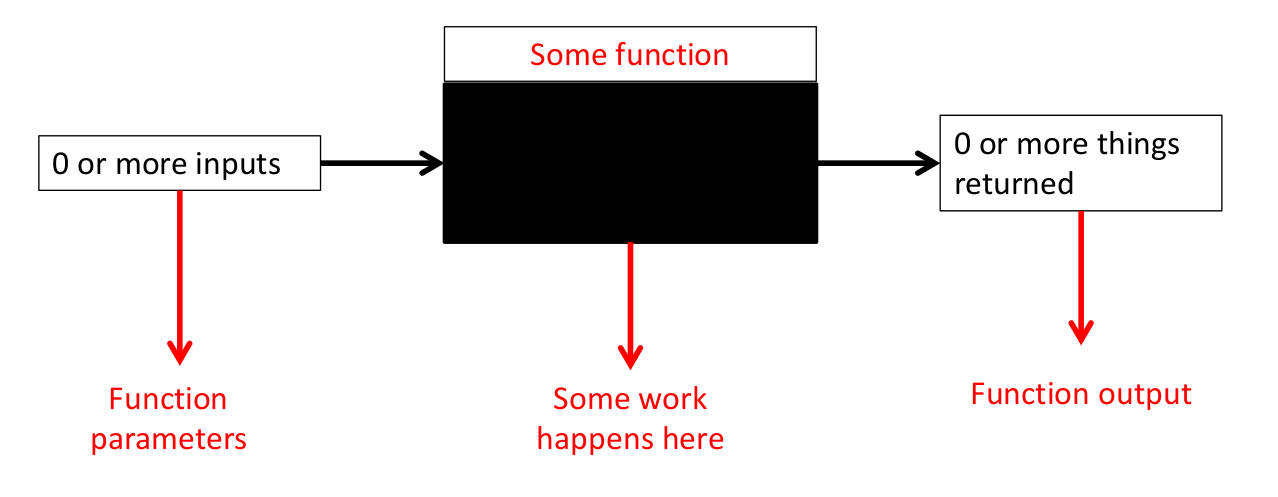
Figure 6.1: Once we have written a function, we don’t care how it works internally. All we care about is what we need to give it, and what it gives us back (if anything)
Functions are a powerful way for writing and reasoning about code for a number of reasons. For one, it embodies the divide and conquer principle by allowing us to chop up a program into manageable pieces, and then tackle them one by one. It also makes programs much easier to read. For example, imagine we have a bunch of functions and then want to use them as follows:
username = input()
password = input()
if is_valid(username, password):
option = show_menu()
process_input(option)
else:
display_warning()We don’t need to look inside the functions to understand what’s roughly going on here — the function names tell us everything we need to know!
On top of that, we’ve already mentioned the reusability aspect — we can reuse a function if the thing it does comes up often. However, it also makes testing code easier (since we can test functions independently of one another), helps with the distribution of labour (I will work on function A, you work on function B), and maintenance (if there’s a problem, we can often isolate with function is causing it and fix things).